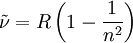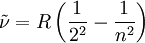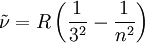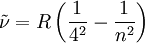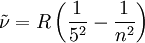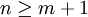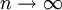Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Balmer-SerieAls Balmer-Serie wird die Folge von Spektrallinien im (elektronischen) Spektrum des Wasserstoffatoms bezeichnet, deren Wellenzahl durch die Formel gegeben ist. Darin ist die nach dem schwedischen Physiker Janne Rydberg benannte Rydberg-Konstante. Für n sind ganze Zahlen größer als 2 einzusetzen. Die Wellenzahl lässt sich durch die Beziehung in die Wellenlänge bzw. durch in die entsprechende Photonenenergie umrechnen. In der letzten Formel sind c die Lichtgeschwindigkeit im Vakuum und h die Planck'sche Konstante. Weiteres empfehlenswertes Fachwissen
Entdeckung der Balmer-LinienIm sichtbaren Bereich des Wasserstoffatom-Spektrums lassen sich vier Linien beobachten. Ihr Abstand nimmt mit der Wellenlänge ab. Sie werden, beginnend mit der größten Wellenlänge, mit Hα, Hβ, Hγ und Hδ bezeichnet. Im Jahr 1885 entdeckte der Schweizer Johann Jakob Balmer, dass sich die Wellenlänge dieser Linien mit der einfachen Formel berechnen lässt: In dieser Gleichung ist A eine rein empirische Konstante (A = 3.645,6 * 10-10 m = 3.645,6 Å), und für n sind die ganzen Zahlen 3, 4, 5 und 6 einzusetzen. Im Ultravioletten, dem für das menschliche Auge nicht sichtbaren Bereich des Spektrums, wurden weitere Linien entdeckt. Diese werden fortlaufend mit Hε, Hζ usw. bezeichnet. Die experimentell bestimmte Wellenlänge dieser Linien stimmt mit den rechnerischen Werten aus der Balmerformel für ganzzahlige n größer 6 ebenfalls sehr gut überein. Verallgemeinerung durch RydbergMit der obigen Beziehung zwischen Wellenlänge und Wellenzahl sowie Bereits 1890 verallgemeinerte Johannes Rydberg die Formel von Balmer zur Rydberg-Formel : Bis zu diesem Zeitpunkt waren im Wasserstoffspektrum nur Linien für m = 2 bekannt, d.h. seine Formel war eine Voraussage für noch nicht gefundene Linien! Die Entdeckung einer neuen Serie für m = 1 durch den US-amerikanischen Physiker Theodore Lyman im Jahr 1906 bestätigte Rydbergs Erweiterung.
Ritz'sches KombinationsprinzipDie Formel von Rydberg beschreibt das Wasserstoffspektrum recht genau. Jedoch bei den meisten anderen Atomen liefert sie keine korrekten Ergebnisse. Einen Fortschritt in der Beschreibung der Atomspektren lieferte im Jahr 1908 der Schweizer Mathematiker Walter Ritz. Er entdeckte das nach ihm benannte Ritzsche Kombinationsprinzip: "Durch additive oder subtraktive Kombination, sei es der Serienformeln selbst, sei es der in sie eingehenden Konstanten, lassen sich andere Serienformeln bilden." Vereinfacht ausgedrückt bedeutet dies, dass sich durch zwei bekannte Linien eine mögliche dritte Linie berechnen lässt. Jedoch nicht alle dieser damit berechneten Linien lassen sich beobachten. Welche Linien auch wirklich auftreten, konnte Ritz nicht erklären. Deutung durch das Bohrsche AtommodellDie bis zu diesem Zeitpunkt rein empirisch gefundenen Formeln ließen sich erstmals mit dem Bohrschen Atommodell verstehen. Danach sind die Spektrallinien auf den Übergang von Elektronen auf ein anderes Energieniveau zurückzuführen. Mit dem Modell von Bohr erhält man als allgemeine Formel für diese Übergänge:
Das erste Glied in der Klammer, 1/m2, ist der so genannte Grundterm. Das zweite, 1/n2, wird als Laufterm bezeichnet. Hält man m im Grundterm fest und variiert n im Laufterm, ergeben sich die unten aufgeführten, nach ihren Entdeckern benannten Serien. Mit Ausnahme von Hα, Hβ, Hγ und Hδ liegen sie im ultravioletten bzw. infraroten Bereich des Frequenzspektrums.
Bereits im Bohrschen Atommodell ist, im Gegensatz zur Balmerformel, die Konstante keine rein empirische Größe. Vielmehr lässt sich der Wert direkt auf in die Rechnung eingehende Naturkonstanten zurückführen. Der Index deutet dabei an, dass die Bewegung von Atomkern und Elektron um den gemeinsamen Schwerpunkt berücksichtigt wurde. Auch die Einschränkung auf ganzzahlige Werte für m und n sowie die Bedingung folgt aus diesem Modell. Die Variablen sind danach Quantenzahlen; m und n sind die Hauptquantenzahlen für den Grundzustand (m) und den angeregten Zustand (n).
Die Abbildung zeigt das Termschema des Wasserstoffatoms und visualisiert die obigen Formeln: Auf der linken vertikalen Achse ist die Hauptquantenzahl m abgetragen. Auf der rechten vertikalen Achse ist die zugehörige Anregungsenergie vom Grundzustand in eV angegeben. Der Abstand der Energieniveaus ist maßstabsgerecht. In horizontaler Richtung sind für jede Serie exemplarisch die ersten Übergänge eingezeichnet. Die zugehörigen Nebenquantenzahlen n sind in kursiver Schrift darüber angegeben. Der Abstand der Linien zueinander, d.h. in horizontaler Richtung, ist nicht maßstabsgerecht, sondern aus Gründen der Übersichtlichkeit gleich groß gewählt. Die Abbildung verdeutlicht, dass alle Linien einer Serie auf dem gleichen Energieniveau enden. Die Hα-Linie der Balmer-Serie ist somit ein Übergang von m = 3 nach m = 2. Ganz rechts in den Serien ist gepunktet die jeweilige Seriengrenze d.h. dargestellt. Das Elektron ist dann nicht mehr an dem Atomkern gebunden, das Atom ist ionisiert. Für die Lyman-Serie erhält man mit der Bohrschen Formel eine Energie von 13,6 eV. Auch dieser Wert stimmt mit dem experimentell bestimmten Wert für die Ionisationsenergie des Wasserstoffatoms im Grundzustand gut überein. Die Frage, welche der Linien, die nach dem Ritzschen Kombinationsprinzip möglich sind, auch tatsächlich auftreten, wird durch die Auswahlregeln geklärt. Diese ergeben sich aus quantenmechanischen Rechnungen. Siehe auch: Nebulium Weitere Serien sind: |
|||||||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Balmer-Serie aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


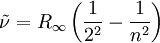
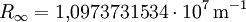
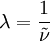
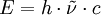



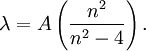
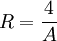 lässt sich die von Balmer gefundene Formel schreiben:
lässt sich die von Balmer gefundene Formel schreiben:
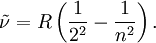
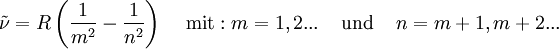
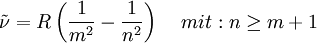 .
.