Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Compton-Effekt
Als Compton-Effekt oder Compton-Streuung (manchmal auch als inkohärente Streuung) bezeichnet man einen physikalischen Streuprozess, bei dem die Wellenlänge von Photonen bei der Streuung an (quasi-) freien Elektronen um einen Wert Δλ vergrößert wird (Frequenz bzw. Energie sinkt). Compton-Streuung tritt immer dann auf, wenn die Energie des Photons vergleichbar ist mit der Ruheenergie des Elektrons, d. h. Compton-Streuung ist der dominierende Wechselwirkungsprozess in Materie für Photonenenergien zwischen ca. 100 keV bis ca. 10 MeV, wobei der tatsächliche Bereich vom Streumaterial abhängt. Bei der Streuung an freien, ruhenden Elektronen gilt für die Änderung der Wellenlänge: Dabei bezeichnet Δλ die Wellenlängenänderung des Photons, h das Plancksche Wirkungsquantum, m0e die Ruhemasse des Elektrons, c die Lichtgeschwindigkeit und Ist das Elektron an ein Atom gebunden, dann gilt diese Formel nur noch näherungsweise, da der ursprüngliche Impulsvektor des Elektrons in der Atomhülle nicht bekannt ist. Den Einfluss dieses Effektes auf die Bestimmung des Streuwinkels bzw. der Ursprungsrichtung des einfallenden Photons bezeichnet man als Doppler-Verbreiterung. Er ist besonders stark ausgeprägt bei niedrigen Energien, großen Streuwinkeln und Atomen mit hoher Kernladungszahl. Aufgrund der Änderung der Energie des Photons und der damit verbundenen Energieübertragung auf das Elektron spricht man von inelastischer (seltener auch von inkohärenter) Photonstreuung, um sie von der elastischen (kohärenten) Photonstreuung (Thomson-Streuung an freien Elektronen, Rayleigh-Streuung an gebundenen Elektronen) zu unterscheiden. Da bei der Compton-Streuung in Materie in der Regel ein Elektron aus der Atomhülle geschlagen wird, zählt Compton-Streuung zu den wichtigsten Prozessen, die zur Ionisation von Materie durch harte Röntgen- und Gammastrahlung führen. Neben dem Compton-Effekt existiert auch der inverse Compton-Effekt. Dabei streut ein relativistisches Elektron an einem Photon geringerer Energie. Dadurch kommt es zum Energieübertrag vom Elektron auf das Photon. Diesen Effekt kann man unter anderem in den Akkretionsscheibenkoronae von aktiven Galaxienkernen beobachten. Weiteres empfehlenswertes Fachwissen
GeschichteBis zur Entdeckung des Compton-Effekts fehlte ein eindeutiger Nachweis, dass Licht tatsächlich, wie von Albert Einstein 1905 postuliert, neben dem Wellencharakter auch Teilchencharakter hat (siehe auch Welle-Teilchen-Dualismus). Als Arthur Holly Compton im Jahre 1922 die Streuung von hochenergetischen Röntgenstrahlen an Graphit untersuchte, machte er zwei Beobachtungen: Zum einen war die Streuwinkelverteilung hinsichtlich Vorwärts- und Rückwärtskomponente nicht symmetrisch, und zum anderen war die Wellenlänge der gestreuten Strahlung nicht mehr identisch mit der der einfallenden Strahlung. Beide Beobachtungen standen im Widerspruch zur klassischen Beschreibung der elastischen Streuung von Licht an freien Elektronen (Thomson-Streuung) und an gebundenen Elektronen (Rayleigh-Streuung), die vom Wellencharakter des Lichts ausgeht. Stattdessen gelang es Compton, nachzuweisen, dass sich die Energie und Richtung des gestreuten (hochenergetischen) Photons wie bei einem klassischen Teilchenstoß zwischen Photon und Elektron aus dem Energie- und Impulserhaltungssatz (siehe Kinematik) bestimmen lassen. Damit bewies Compton den Teilchencharakter von Licht. [1] [2] Für die Entdeckung des nach ihm benannten Effekts erhielt Compton im Jahre 1927 den Nobelpreis für Physik. AnwendungenDa es sehr schwierig ist, Gammastrahlung mittels Linsen zu fokussieren, spielt der Compton-Effekt eine wichtige Rolle bei der Abbildung mittels Gammastrahlen im Energiebereich von einigen hundert keV bis zu einigen zehn MeV. In sogenannten Compton-Teleskopen (auch Compton-Kameras genannt) misst man Energie und Richtung des gestreuten Photons sowie Energie und (manchmal) auch Richtung des Elektrons. So können Energie, Ursprungsrichtung und unter Umständen die Polarisation des einfallenden Photons bestimmt werden. In der Realität wird dies durch Messunsicherheiten und nicht gemessene Größen wie die Richtung des Elektrons jedoch stark erschwert, so dass komplexe Ereignis- und Bildrekonstruktionsmethoden angewandt werden müssen. Das wohl bekannteste Compton-Teleskop war COMPTEL, das an Bord des NASA-Satelliten CGRO von 1991 bis 2000 als erstes Teleskop den Sternenhimmel im Energiebereich zwischen 0,75 und 30 MeV erforschte. Zu den Erfolgen von COMPTEL zählen u. a. die Erstellung der ersten Himmelskarten in diesem Energiebereich, die Erforschung der Nukleosynthese z. B. von radioaktivem 26Al (massereiche Sterne und Supernovae) und 44Ti sowie Fortschritte bei der Erforschung von Pulsaren, Aktiven Galaxien (AGNs) etc. Es laufen Entwicklungsarbeiten zum Einsatz von Compton-Kameras im Bereich der Medizin oder Nukleartechnik. In der Medizin könnten sie gegenüber den heute verwendeten Szintigraphie-Gammakameras Bilder mit besserer räumlicher Auflösung liefern, also Tumore und Metastasen exakter lokalisieren. In der Nukleartechnik könnten in Zukunft mittels Compton-Kameras z. B. Nuklearanlagen oder nukleare Abfälle überwacht werden. Im Bereich der Flugsicherung wurden Scanner-Geräte entwickelt, welche die Compton-Rückstreuung (engl. Backscatter) normaler Röntgenstrahlen an Oberflächen nutzen. Diese werden zur Zeit in den USA getestet. Compton-Wellenlänge, Compton-Spektrum und Compton-Kante
Die Wellenlängenänderung des Photons vor und nach dem Stoß hängt nur vom Streuwinkel und wird als „Compton-Wellenlänge des Elektrons“ bezeichnet. Die relativ geringe Änderung ist die Ursache dafür, dass der Compton-Effekt nur bei kurzwelliger Strahlung wie Röntgen- oder Gammastrahlung beobachtet werden kann.
Die maximale Änderung der Wellenlänge tritt bei einem Winkel von Werden viele γ-Quanten der Energie hν nach Compton gestreut (z. B. in einem Szintillator), so ergibt sich ein charakteristisches Energiespektrum der gestreuten Elektronen, wie es in der nebenstehenden Graphik gezeigt wird. Die hierbei auf die Elektronen übertragene Energie ist wegen der Abhängigkeit vom Streuwinkel
Das Atom ist nach der Compton-Streuung ionisiert. Zusätzlich erhält man im Elektronenspektrum einen „Peak“ (Spektrallinie) bei der Energie hν. In diesem Fall wird also die gesamte Energie des Photons auf das Elektron übertragen. Dies ist kein Compton-Effekt mehr, sondern der Photoeffekt. Anmerkung
Photonen, die auf gebundene Elektronen oder Atomkerne treffen, ändern zwar ihre Bewegungsrichtung, nicht aber ihre Frequenz/Wellenlänge, da die festen Teilchen praktisch keine kinetische Energie erhalten. Dadurch besteht die gestreute Strahlung neben der durch den Compton-Effekt langwelligeren Strahlung auch zu einem Anteil aus Strahlung mit der Ausgangswellenlänge (Thomson-Streuung), deren Intensität vom Ablenkwinkel abhängt. Man beachte, dass für energiereichere Strahlung (beispielsweise Röntgenstrahlung) auch die Hüllenelektronen näherungsweise als frei angesehen werden können. Beim Compton-Effekt handelt es sich um einen Bruch mit der klassischen Physik. Der klassischen Physik nach müssten die Elektronen durch das Licht nicht angestoßen werden, sondern auf Grund des Wellencharakters des Lichts in Schwingungen versetzt werden, also zu Dipolen werden, welche Strahlung der gleichen Wellenlänge wie das einfallende Licht aussenden. Messungen ergaben, dass dies nicht der Fall ist. Hingegen ist die Comptonstreuung einwandfrei als Stoßprozess zwischen Photon und (quasi-) freiem Elektron beschreibbar. Dies ist ein Beweis dafür, dass Lichtstrahlung auch Teilcheneigenschaften hat (siehe Welle-Teilchen-Dualismus).
Herleitung der GleichungBei den unterschiedlichen Herleitungen wird immer ein freies Elektron angenommen. Ist das Elektron in einem Atom gebunden, muss man die Bindungsenergie von der kinetischen Energie des Elektrons nach dem Stoß abziehen. Ruhesystem des ElektronsIm Ruhesystem eines Elektrons wird das Elektron vor dem Stoß als ruhend angenommen. Das Photon überträgt beim Zusammenstoß Energie an das Elektron. Nach dem Stoß bewegt sich das Elektron. Da die Geschwindigkeit des Photons stets die Lichtgeschwindigkeit ist, muss es seine Energie ändern, um die Impulserhaltung zu erfüllen.
Einsetzen des Energieerhaltungs- und Kosinussatzes in die Energie-Impuls-Beziehung:
SchwerpunktsystemBei der Streuung des Photons am Elektron verliert das Photon in Abhängigkeit vom Streuwinkel Energie und vergrößert entsprechend seine Wellenlänge. Eine Vergrößerung der Wellenlänge eines Photons ist aber eine ungewöhnliche Eigenschaft, da Photonen ihre Energie nur vollständig abgeben können. Dieser Widerspruch lässt sich auflösen, wenn man den Vorgang als Streuung im Schwerpunkt von Photon und Elektron beschreibt. Im Schwerpunktsystem wird das Photon mit der Wellenlänge λ1 reflektiert und ändert seine Wellenlänge nicht. Hierfür muss man das Bezugssystem in den Schwerpunkt verlegen, wobei sich wegen des Dopplereffekts die Wellenlänge λ1 ergibt. Im Schwerpunktsystem wird das Photon um den Winkel β gestreut, seine Wellenlänge λ1 behält es bei. Das Elektron wird ebenfalls um den Winkel β gestreut und behält im Betrag seine Geschwindigkeit vs. Die Summe der Einzelimpulse ergibt vorher und nachher 0. Die Schwerpunktsgeschwindigkeit ist
wobei Die Wellenlänge im Schwerpunktsystem ergibt sich über den relativistischen Dopplereffekt zu
Die Geschwindigkeit c des Photons mit der Wellenlänge λ1 enthält die beiden Komponenten vpx und vpy , die dann über eine relativistische Geschwindigkeitsaddition ins Laborsystem mit den Geschwindigkeiten vx und vy übertragen werden. Ebenso verfährt man mit den Geschwindigkeitskomponenten des Elektrons vsx und vsy , die nach vex und vey im Laborsystem transformiert werden.
Geschwindigkeiten des Elektrons im Schwerpunktsystem
Geschwindigkeiten des Photons im Schwerpunktsystem
Geschwindigkeiten des Photons im Laborsystem
Geschwindigkeiten des Elektrons im Laborsystem
Für den Streuwinkel des Photons gilt
Die Wellenlänge λ’ erhält man über die Energieerhaltung,
oder über den Dopplereffekt bzw. der Compton-Gleichung. Das Schwerpunktsystem eignet sich also als Bezugssystem für Stoßprozesse. Beliebiges BezugssystemBetrachtet man den Compton-Effekt aus einem beliebigen Bezugssystem, so hat das Elektron auch vor dem Stoß eine Geschwindigkeit. Die Gesamtenergie des Elektrons ist Ee = γm0ec2 und sein Impuls lautet Die Viererimpulse, die die beteiligten Teilchen vor und nach dem Streuprozess besitzen, sind Photon vor der Streuung: Elektron vor der Streuung: Photon nach der Streuung: Elektron nach der Streuung: wobei
wobei zu beachten ist, dass
Hierbei ist Ω der Winkel zwischen Elektron und Photon vor der Streuung. Analog erhält man
wobei Ω' der Winkel zwischen dem Elektron vor der Streuung und dem Photon nach der Streuung ist.
wobei α der Winkel zwischen dem Photon vor der Streuung und dem Photon nach der Streuung ist. Wird ein Photon an einem Elektron gestreut, so muss die Energie- und Impulserhaltung erfüllt sein. Da die Energie die Nullkomponente des Vierimpulses ist und die restlichen Komponenten den Impuls repräsentieren, folgt
Unter Verwendung von
Nach Einsetzen der Komponenten erhält man Je nach Einfallswinkel und kinetischer Energie, kann das Elektron eine gewisse Menge Energie an das Photon übertragen (inverse Compton- Streuung). Im Ruhesystem des Elektrons ist die Geschwindigkeit desselben vor dem Stoß Null. Demnach ist
womit sich die bekannte Formel ergibt. Quellen und Referenzen |
||||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Compton-Effekt aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


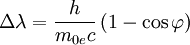
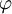 den Streuwinkel des Photons.
den Streuwinkel des Photons.



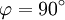 ist
ist
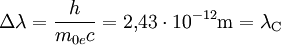
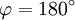 auf. Das Photon wird in die ursprüngliche Richtung zurückgestreut (Rückstoß).
Diese entspricht
auf. Das Photon wird in die ursprüngliche Richtung zurückgestreut (Rückstoß).
Diese entspricht 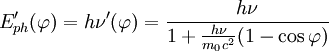
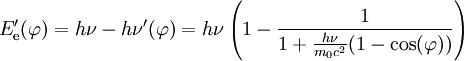
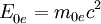
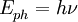
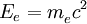
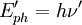
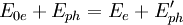
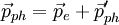
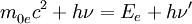
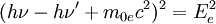
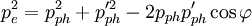
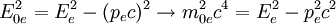
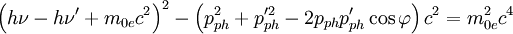
![\left(h\nu-h\nu'+m_{0e}c^2\right)^2-\left[\left(\frac{h\nu}{c}\right)^2+\left(\frac{h\nu'}{c}\right)^2-2\left(\frac{h\nu}{c}\right)\left(\frac{h\nu'}{c}\right) \cos \varphi\right]c^2=m_{0e}^2c^4](images/math/d/7/d/d7de3a86c906c0f30f7c6a042678e840.png) , mit
, mit 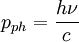
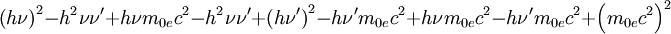
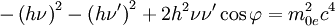
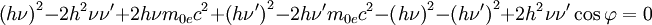
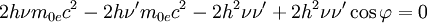
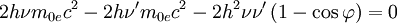
![2h\left[m_{0e}c^2\left(\nu-\nu'\right)\right]=2h^2\nu\nu'\left(1- \cos \varphi \right)](images/math/f/b/f/fbfedcb2c8608dabeb0c46acc0e043df.png)
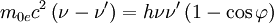
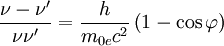
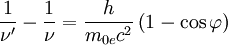
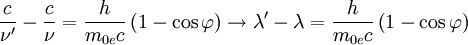
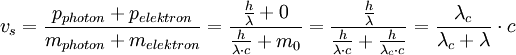
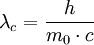 die Comptonwellenlänge ist.
die Comptonwellenlänge ist.
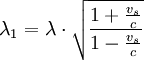 .
.
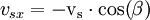
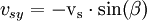
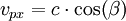
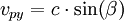
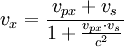
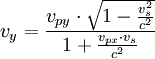
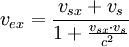
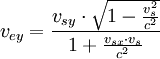
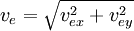 ,
,
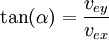 .
.
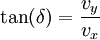 , mit
, mit 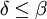 .
.
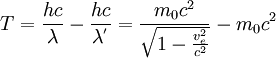
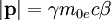 .
.
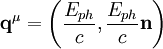
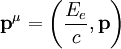
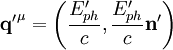
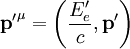 ,
,
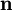 der Einheitsvektor in Bewegungsrichtung des Photons ist. Die Quadrate der Impulse ergeben sich bekanntlich zu
der Einheitsvektor in Bewegungsrichtung des Photons ist. Die Quadrate der Impulse ergeben sich bekanntlich zu
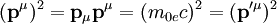
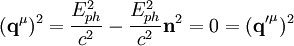 ,
,
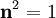 gilt.
gilt.
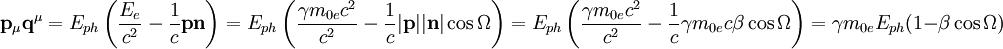 .
.
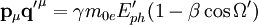 ,
,
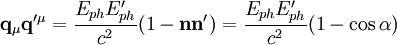 ,
,
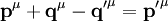
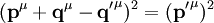
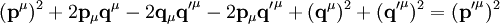 .
.
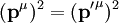 , sowie
, sowie 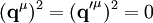 vereinfacht sich dies zu
vereinfacht sich dies zu
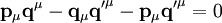 .
.