Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Dichtefunktionaltheorie (Quantenphysik)Die Dichtefunktionaltheorie (DFT) ist ein Verfahren zur Bestimmung des quantenmechanischen Grundzustandes eines Vielelektronensystems, das auf der (ortsabhängigen) Dichte der Elektronen beruht. Die Dichtefunktionaltheorie wird zur Berechnung grundlegender Eigenschaften von Molekülen und Festkörpern wie beispielsweise von Bindungslängen und der Bindungsenergie verwendet. Die große Bedeutung der Dichtefunktionaltheorie liegt darin, dass es damit nicht notwendig ist, die vollständige Schrödingergleichung für das Vielelektronensystem zu lösen, und dadurch der Aufwand an Rechenleistung stark sinkt beziehungsweise Berechnungen von Vielelektronensystemen mit deutlich über 10 Elektronen überhaupt erst möglich werden. Für die Entwicklung der Dichtefunktionaltheorie wurde im Jahr 1998 der Nobelpreis für Chemie an Walter Kohn vergeben. Weiteres empfehlenswertes Fachwissen
GrundlagenGrundlage der Dichtefunktionaltheorie ist das Hohenberg-Kohn-Theorem: Der Grundzustand eines Systems von N Elektronen hat eine eindeutige ortsabhängige Elektronendichte Die Rechnungen mit der Dichtefunktionaltheorie werden normalerweise in der Born-Oppenheimer-Näherung durchgeführt, es werden also nur die Elektronen quantenmechanisch behandelt. Die Kohn-Sham-FunktionenUm die Elektronendichte zu bestimmen, werden N Einelektronen-Wellenfunktionen, die sogenannten Kohn-Sham-Funktionen (Anmerkung: in dieser und den folgenden Gleichungen werden der Einfachheit halber atomare Einheiten verwendet. In diesem Einheitensystem erhält man die Energie ε in Hartree.) Die Dichte erhält man aus der Summe der Elektronendichten der Kohn-Sham-Funktionen: Das effektive Potential ist von der Dichte abhängig: Hierbei ist der erste Term, Da das effektive Potenzial Streng genommen sind die Kohn-Sham-Funktionen reine Rechengrößen und haben für sich alleine keine physikalische Bedeutung. In der Praxis können sie jedoch oft als Näherung für tatsächliche Elektronenzustände herangezogen werden, und ihre Energien εj werden z.B. zur Berechnung der Bandstruktur herangezogen. Das Austausch-Korrelations-PotenzialMit dem Kohn-Sham Formalismus wurde das Problem des Vielelektronensystems eigentlich nur auf den Austausch-Korrelationsterm Lokale Dichtenäherung (Engl. local density approximation, LDA): Bei dieser Näherung wird angenommen, dass die Gradienten-Näherung (generalized gradient approximation, GGA): Es werden nicht nur die Dichte Hybrid-Methoden: Hier wird nur ein Teil des Austausch-Korrelations-Potenzials entsprechend der Dichtefunktionaltheorie berechnet (z.B. mit GGA), ein Teil wird als Austausch-Energie der Kohn-Sham-Funktionen wie in der Hartree-Fock-Methode berechnet. Diese Verfahren sind vor allem bei Molekülen genauer als reine GGA-Rechnungen, allerdings ist der Aufwand für die Rechnungen wesentlich höher als bei GGA. Das verbreitetste Hybrid-Verfahren ist als B3LYP bekannt. Die meisten Einschränkungen und Probleme bei der Verwendung der Dichtefunktionaltheorie hängen mit dem Austausch-Korrelations-Potenzial zusammen. So liefern beispielsweise die verschiedenen GGA-Potenziale Bindungsenergien von einfachen Molekülen, die sich voneinander und von den experimentellen Werten um mehr als 20% unterscheiden können. Van-der-Waals-Bindungen werden von den "semilokalen" Funktionen wie GGA überhaupt nicht beschrieben, weil sie auf langreichweitigen Korrelationen der Ladungsverteilung beruhen. Ein weiteres Problem liegt darin, dass die Bandlücken und HOMO-LUMO-Energiedifferenzen, die aus den Kohn-Sham Funktionen berechnet werden, bei LDA und GGA generell zu niedrig sind. Rechenverfahren am ComputerBerechnungen komplexer Strukturen mittels Dichtefunktionaltheorie erfordern hohe Computerleistung, daher kommt einer effizienten Durchführung der Rechnungen große Bedeutung zu. Die Rechenverfahren können nach den Basisfunktionen für die Kohn-Sham Gleichungen eingeteilt werden: Atomare Wellenfunktionen in einer kugelförmigen Umgebung um den Atomkern (sog. muffin tin-Bereich) sind gut zur Beschreibung der Elektronen in Kernnähe geeignet, allerdings ergeben sich Probleme, die Elektronen zwischen den Atomen (z.B. Leitungselektronen in Metallen) beziehungsweise den Überlappungsbereich zwischen den Atomen konsistent zu beschreiben. Ebene Wellen sind gut zur Beschreibung der Valenzelektronen und Leitungselektronen in Festkörpern geeignet, jedoch können die räumlich wenig ausgedehnten Wellenfunktionen nahe an den Atomkernen schlecht beschrieben werden. Ebene Wellen haben jedoch den Vorteil, dass effiziente Algorithmen zur Fouriertransformation eingesetzt werden können und dadurch die Lösung der Kohn-Sham Gleichungen sehr rasch erfolgen kann. Ein weiterer Vorteil ebener Wellen ist, dass damit die Kräfte zwischen Atomen relativ einfach berechnet werden können. Vor allem für Berechnungen in der Festkörperphysik werden daher diese Verfahren kombiniert, indem man ebene Wellen verwendet, für den Bereich nahe den Atomkernen aber zusätzliche Maßnahmen trifft. Dieser Bereich kann entweder vollständig getrennt behandelt werden (augmented plane waves), es können dort zusätzliche Wellenfunktionen addiert werden (projector augmented waves) oder es kann ein sogenanntes Pseudopotential verwendet werden, das nur im Bereich der Außenelektronen korrekte Wellenfunktionen ergibt, aber nicht in der Nähe der Atomkerne. Gauß-Funktionen und Funktionen mit tabellierter Abhängigkeit vom Radius (ausgehend vom Atomkern) werden oft für Berechnungen an Molekülen eingesetzt. Mit leistungsfähigen Computern können heute Systeme von bis zu ca. 1000 Atomen mittels DFT-Rechnungen behandelt werden. Für größere Systeme müssen andere Näherungsverfahren wie die Tight-Binding-Methode oder auf DFT-Ergebnissen basierende Näherungsverfahren verwendet werden. Damit können über 106 Atome behandelt werden. AnwendungenDFT-Rechnungen liefern unmittelbar die Gesamtenergie der Atomkonfiguration und können daher dazu dienen, von mehreren möglichen Anordnungen die energetisch günstigste herauszufinden. Es muss dazu normalerweise die Geometrie jeder Anordnung optimiert werden, das heißt, es werden die Atome so lange verschoben, bis die Kräfte verschwinden bzw. ein Minimum der Energie gefunden ist. Mit den Wechselwirkungspotenzialen bzw. Kräften auf die Atome können Molekulardynamik-Rechnungen durchgeführt werden. Dadurch werden beispielsweise genaue Rechnungen zum Verhalten von Flüssigkeiten oder die Berechnung der Atombewegungen bei chemischen Reaktionen möglich. Allerdings sind solche Rechnungen wegen des hohen Aufwands an Computerleistung auf die Simulation sehr kurzer Zeiträume (Picosekunden) beschränkt. Aus den Kräften auf die Atome bei einer Auslenkung aus ihrer Ruhelage lassen sich die Schwingungsspektren bestimmen und mit dem Experiment vergleichen. Ebenso lassen sich, soweit die Kohn-Sham-Funktionen eine ausreichend gute Näherung für die tatsächlichen Elektronenzustände sind, Photoelektronenspektren berechnen. Da die Wechselwirkung eines Moleküls oder Festkörpers mit elektromagnetischen Feldern im Wesentlichen durch die Elektronen bestimmt wird, können mittels DFT auch die frequenzabhängige Dielektrizitätskonstante und damit zusammenhängende Größen berechnet werden. Erweiterungen der Dichtefunktionaltheorie ermöglichen es, die in der Schrödingergleichung und daher in der Grundform der DFT nicht enthaltenen magnetischen Eigenschaften zu berechnen (Entweder nur durch Aufspaltung in zwei Elektronendichten für die beiden Richtungen des Elektronenspins oder unter Berücksichtigung der Spin-Bahn-Kopplung. Eine weitere Erweiterung der DFT ist die zeitabhängige DFT (time-dependent density functional theory, TDDFT) für die Berechnung angeregter Zustände. Weblinks (englisch)
Kategorien: Quantenphysik | Quantenmechanik | Quantenchemie | Theoretische Chemie | Computerchemie |
|
| Dieser Artikel basiert auf dem Artikel Dichtefunktionaltheorie_(Quantenphysik) aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





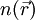 . In der Dichtefunktionaltheorie wird nun die Elektronendichte im Grundzustand bestimmt, daraus können im Prinzip alle weiteren Eigenschaften des Grundzustandes bestimmt werden. Diese Eigenschaften, beispielsweise die Gesamtenergie, sind also Funktionale der Dichte.
. In der Dichtefunktionaltheorie wird nun die Elektronendichte im Grundzustand bestimmt, daraus können im Prinzip alle weiteren Eigenschaften des Grundzustandes bestimmt werden. Diese Eigenschaften, beispielsweise die Gesamtenergie, sind also Funktionale der Dichte.
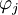 angesetzt, die
angesetzt, die 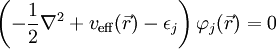
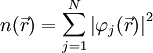
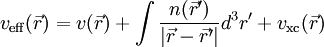
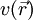 , das externe Potenzial, das im Wesentlichen die Anziehung der Elektronen durch die Atomkerne beschreibt, und der zweite Term beschreibt die elektrostatische Wechselwirkung der Elektronen untereinander (Hartree-Term). Der dritte Term
, das externe Potenzial, das im Wesentlichen die Anziehung der Elektronen durch die Atomkerne beschreibt, und der zweite Term beschreibt die elektrostatische Wechselwirkung der Elektronen untereinander (Hartree-Term). Der dritte Term 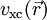 , das sogenannte
, das sogenannte 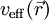 einerseits in den Kohn-Sham-Gleichungen vorkommt, andererseits von der Dichte
einerseits in den Kohn-Sham-Gleichungen vorkommt, andererseits von der Dichte 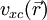 verlagert, und noch nicht gelöst. Streng genommen hängt
verlagert, und noch nicht gelöst. Streng genommen hängt 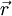 ab, und lässt sich nur für sehr wenige triviale Fälle genau berechnen. Es zeigt sich aber, dass es oft ausreicht, eine näherungsweise Lösung für diesen Term zu finden:
ab, und lässt sich nur für sehr wenige triviale Fälle genau berechnen. Es zeigt sich aber, dass es oft ausreicht, eine näherungsweise Lösung für diesen Term zu finden:


