Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Elektrisches Feld
Weiteres empfehlenswertes FachwissenDas elektrische Feld ordnet jedem Raumpunkt die richtungsabhängige Größe der elektrischen Feldstärke Die Feldstärke ist also, anders gesagt, die Kraft pro Ladungseinheit. Das elektrische Feld ist ein Vektorfeld. Die SI-Einheit von Elektrische Felder gehen von elektrischen Ladungen aus oder entstehen durch Induktion in veränderlichen Magnetfeldern. Licht und andere elektromagnetische Wellen bestehen aus miteinander verketteten elektrischen und magnetischen Feldern. Aufgrund der engen Beziehung zwischen elektrischem und magnetischem Feld fasst man beide in der Elektrodynamik zum elektromagnetischen Feld zusammen. Wenn Richtung und Betrag der elektrischen Feldstärke in jedem Punkt gleich sind, die Feldlinien also parallele Geraden sind, heißt das Feld homogen, sonst inhomogen. Das Feld im Inneren eines Plattenkondensators ist näherungsweise homogen (siehe unten). Zeitlich unveränderliche Felder (siehe Elektrostatik) heißen auch stationäre Felder. Das elektrische Feld in allgemeiner Form ist sowohl orts- als auch zeitabhängig, Homogenes elektrisches FeldDie Stärke des E-Feldes zwischen zwei (streng genommen unendlich großen) planparallelen Kondensatorplatten beträgt Die Ladungen Q auf den Kondensatorplatten verteilen sich dabei gleichmäßig auf den einander zugewandten Plattenaußenseiten. Hier gilt: Da die Flächenladungsdichte als Siehe auch
|
||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Elektrisches_Feld aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. | ||||||||||||||||||||





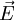 zu. Diese ist definiert durch die Kraft
zu. Diese ist definiert durch die Kraft 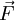 , die auf eine in dem Punkt befindliche Ladung Q wirkt:
, die auf eine in dem Punkt befindliche Ladung Q wirkt:
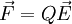
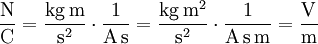
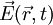 . Es ist über die
. Es ist über die 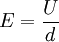 . Dabei ist d der Abstand zwischen den Platten und U die Spannung zwischen den beiden Platten.
. Dabei ist d der Abstand zwischen den Platten und U die Spannung zwischen den beiden Platten.
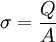 ,
, 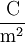 , Q ist die Ladung in C und A die Fläche in m². Diese Flächenladungsdichte wird auch als
, Q ist die Ladung in C und A die Fläche in m². Diese Flächenladungsdichte wird auch als 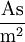 ist die selbe wie
ist die selbe wie 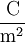 .
.
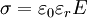 (
( 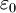 :
: 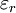 :
: 

