Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
GraphenAls Graphen, englisch Graphene, Betonung Graph-én, bezeichnet man monoatomar dünne Schichten von sp2-hybridisiertem Kohlenstoff. Weiteres empfehlenswertes FachwissenWie bei Alkenen oder Benzen verweist die Endung en des Namens auf ungesättigte Doppelbindungen in den Kohlenstoff-Ringen. Graphen-Flächeneinkristalle sind außerordentlich steif und fest. Die Steifigkeit beträgt wie beim Graphit entlang der Basalebenen ca. 1020 GPa und ist fast so groß wie die des Diamants. Die Darstellung von Graphen erfolgt durch Aufspalten von Graphit in seine Basalebenen. Dabei wird zunächst Sauerstoff interkaliert. Das Diagramm rechts zeigt vier Graphit-Basalebenen eingezeichnet. Die blauen Kugeln stehen für Sauerstoff. Der Sauerstoff reagiert partiell mit dem Kohlenstoff und führt zu einer gegenseitigen Abstoßung der Schichten. Anschließend werden die Graphene suspendiert und je nach Verwendungszweck zum Beispiel in Polymeren eingebettet. Eine weitere Möglichkeit der Darstellung einzelner Graphen-Lagen ist das Erhitzen hexagonaler Siliziumkarbid-Oberflächen auf Temperaturen oberhalb 1400°C. Aufgrund des höheren Dampfdruckes des Siliziums evaporieren die Silizium-Atome schneller als die Kohlenstoff-Atome. Auf der Oberfläche bilden sich dann dünne Schichten einkristallinen Graphits, die aus wenigen Graphen-Monolagen bestehen. Neben den Anwendungsmöglichkeiten in Verbundwerkstoff dient Graphen in der Grundlagenforschung als Modellsubstanz für zweidimensionale Kristalle. Der Ein-Elektron-Transistor aus Graphen könnte Silizium als Transistormaterial ablösen. [1] EigenschaftenDie elektrischen Eigenschaften von Graphen lassen sich gut durch ein Tight-Binding-Modell beschreiben. Im Rahmen dieses Modells ergibt sich die Energie der Elektronen mit Impuls
mit
der Nächsten-Nachbar-Hopping-Energie
Hier bezeichnet Literatur
Quellen
Kategorien: Nanowerkstoff | Stoffgruppe |
| Dieser Artikel basiert auf dem Artikel Graphen aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





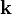 zu
zu
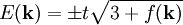
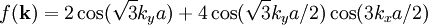 ,
,
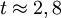 eV und der Gitterkonstante
eV und der Gitterkonstante 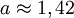 Å.
Å.
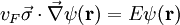
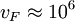 m/s die
m/s die 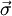 die
die 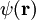 die zweikomponentige
die zweikomponentige 

