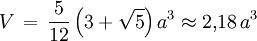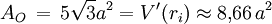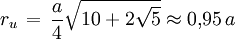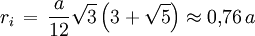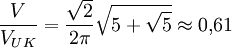Ikosaeder

Das Ikosaeder [ikosaˈeːdər] (nach griech. εἰκοσάεδρον eikosáedron = Zwanzigflächer) ist einer der fünf platonischen Körper, genauer: ein Polyeder (ein Vielflächner) mit

• zwanzig (kongruenten) gleichseitigen Dreiecken als Flächen
• dreißig (gleich langen) Kanten und
• zwölf Ecken, in denen jeweils fünf Flächen zusammentreffen

Weiteres empfehlenswertes Fachwissen

Empfindlichkeitsprüfung von Laborwaagen

Wie erhalten Sie Tag für Tag genaue Wägeresultate?

Leitfaden zu den grundlegenden Laborkenntnissen

Symmetrie

Wegen seiner hohen Symmetrie – alle Ecken, Kanten und Flächen sind untereinander gleichartig – ist das Ikosaeder ein reguläres Polyeder. Es hat:

• sechs fünfzählige Drehachsen (durch gegenüber liegende Ecken)
• zehn dreizählige Drehachsen (durch die Mittelpunkte gegenüber liegender Flächen)
• fünfzehn zweizählige Drehachsen (durch die Mittelpunkte gegenüber liegender Kanten)
• fünfzehn Symmetrieebenen (durch einander gegenüber liegende – und parallele – Kanten)

und ist

• zentralsymmetrisch (Punktspiegelung am Mittelpunkt des Polyeders)

Insgesamt hat die Symmetriegruppe des Ikosaeders – die Ikosaeder- oder Dodekaedergruppe – 120 Elemente. (Manchmal wird jedoch auch die Untergruppe der Drehungen des Ikosaeders in sich Ikosaedergruppe genannt. Diese Untergruppe hat die Ordnung 60 und ist die kleinste nichtabelsche einfache Gruppe). Die Symmetrie des Ikosaeders ist (wegen der bei ihm auftretenden fünfzähligen Symmetrie) mit einer periodischen Raumstruktur nicht verträglich. Es kann daher kein Kristallgitter mit Ikosaedersymmetrie geben (vgl. jedoch Quasikristalle).

Beziehungen zu anderen Polyedern

    Das Pentagondodekaeder ist das zum Ikosaeder duale Polyeder (und umgekehrt).
Mit Hilfe von Ikosaeder und Dodekaeder können zahlreiche Körper konstruiert werden, die ebenfalls die Ikosaedergruppe als Symmetriegruppe haben. So erhält man zum Beispiel

• ein abgestumpftes Ikosaeder mit 20 Sechsecken und 12 Fünfecken, ähnlich einem Fußball (siehe unten), siehe auch Fulleren
• ein Ikosidodekaeder mit 20 Dreiecken und 12 Fünfecken
• ein abgestumpftes Dodekaeder mit 20 Dreiecken und 12 Zehnecken als Durchschnitte eines Ikosaeders mit einem Dodekaeder (siehe archimedische Körper) und
• ein Rhombentriakontaeder mit 20+12 = 32 Ecken und 30 Rhomben als Flächen als konvexe Hülle einer Vereinigung eines Ikosaeders mit einem Dodekaeder.

(Ikosa gri. für 20) Spezialfall „Fußball“ — abgestumpftes Ikosaeder Die Form eines Fußballs stellt einen Spezialfall des Ikosaeders dar, das abgestumpfte Ikosaeder. Ein abgestumpftes Ikosaeder ist ein Körper, der von 12 regelmäßigen Fünfecken und 20 regelmäßigen Sechsecken gebildet wird. Er sieht aus wie ein Ikosaeder, dem gleichmäßig die Ecken abgeschnitten wurden. ^[1]

Zur Struktur des Ikosaeders

Wie die untenstehende Graphik zeigt, kann man unter den Kanten des Ikosaeders drei Paare gegenüber liegender (also insgesamt sechs) Kanten so auswählen, dass diese Paare drei kongruente zueinander paarweise orthogonale Rechtecke aufspannen. (Die Längen der Seiten dieser Rechtecke entsprechen dem Goldenen Schnitt, weil sie Seiten bzw. Diagonalen regelmäßiger Fünfecke sind.) Das Ikosaeder kann daher so in einen Würfel eingeschrieben werden, dass diese sechs Kanten in den sechs Flächen des Würfels liegen und parallel zu den Kanten des Würfels sind.
Die 24 restlichen Kanten begrenzen 8 Dreiecke (unter den 20 Flächen des Ikosaeders), die in den Flächen eines – dem Ikosaeder umschriebenen – Oktaeders liegen, wobei die Ecken des Ikosaeders auf dessen Kanten liegen.
Insgesamt gibt es fünf derartige Positionen, wobei jede Kante des Ikosaeders zu genau einer solchen Gruppe von orthogonalen Kantenpaaren gehört, während jede Fläche zweimal in der Fläche eines umschriebenen Oktaeders liegt. Die Symmetriegruppe des Ikosaeders bewirkt alle 5!=120 Permutationen dieser fünf Positionen.

Die Kanten des Ikosaeders enthalten zwölf ebene Fünfecke, wobei jede Kante zu zwei und jede Ecke zu fünf dieser Fünfecke gehört. Man kann diese Eigenschaft zum Bau eines Drahtmodells benutzen.

Formeln

Größen eines Ikosaeders mit Kantenlänge a
Volumen
Oberflächeninhalt
Umkugelradius
Inkugelradius
Verhältnis von Volumen zu Umkugelvolumen

Bedeutung des Ikosaeders in der Clusterphysik

Große Bedeutung hat die Ikosaeder-Form bei Clustern (Ansammlungen von Atomen in der Größenordnung von 3 bis 50000 Atomen) ab einer Größe von mehr als 7 Atomen. Grund dafür ist die Regel von Friedel, die besagt, dass diejenige Struktur die geringste Energie besitzt, für die die Anzahl der Nächste-Nachbarn-Bindungen maximal ist. Bei vielen freien Clustern tritt dies ab 7 Atomen auf, wobei es allerdings auch Ausnahmen gibt und andere Strukturen bevorzugt werden (etwa Kuben).

Des Weiteren gibt es in der Clusterphysik sogenannte magische Zahlen, die eng mit dem sogenannten Mackayschen Ikosaeder zusammenhängen. Hier sorgen Schalenabschlüsse (also perfekte Atom-Ikosaeder) für besonders stabile Cluster. Dies tritt bei Clustern mit den magischen Atomzahlen 13, 55, 147, 309, 561, 923 und 1415 auf. Diese recht alten Erkenntnisse von A.L. Mackay ^[2] spielen in der aktuellen Clusterphysik eine bedeutende Rolle.

Anwendungen

• Die Capside vieler Viren haben eine ikosaedrische Symmetrie. Das ist dadurch zu erklären, dass Viren ihre Nukleinsäure optimal verpacken. Die Ikosaederform ist in dieser Hinsicht günstig, weil das Ikosaeder von allen regelmäßigen Polyedern mit gegebenem Durchmesser das größte Volumen besitzt.
• Rudolf von Laban hatte das Ikosaeder für seine Raumharmonielehre intensiv genutzt und beeinflusste damit den modernen Tanz. Dies wird heute in der "Laban Movement Analysis" weiter geführt.
• Stafford Beer hatte in seiner kybernetischen Managementtheorie die Ikosaeder-Struktur als Modell für eine optimale Vernetzung von Mitarbeitern in Teams herausgearbeitet.
• In vielen Rollenspielen werden Ikosaeder als zwanzigseitige Spielwürfel (W20) verwendet.

Quellen

1. ↑ Mathematische Basteleien - Fußball: [1]
2. ↑ Acta Crystallographia 15, 916 (1962)