Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Innere EnergieAls innere Energie bezeichnet man den in einem Medium gebundenen Energiebetrag. Die innere Energie ist der Energiegehalt einer Materiemenge, der über ihre geordnete kinetische Energie und potentielle Energie des Schwerpunktes hinausgeht. Sie ergibt sich aus den inneren Eigenschaften eines Systems teilweise auch unter dipolartiger Wechselwirkung mit äußeren Feldern. Weiteres empfehlenswertes FachwissenJe mehr über den Aufbau der Materie bekannt wurde, desto mehr Ursachen für die innere Energie wurden erkannt. Man unterscheidet den physikalisch-thermischen, den chemischen und den kernphysikalischen Anteil der inneren Energie sowie die Wechselwirkungen mit äußeren Feldern. Die Summe aus Lage-, Bewegungs- und Spannenergie ist bei reibungsfreien Vorgängen in einem abgeschlossenen System konstant.
Der Erste Hauptsatz der Thermodynamik beschreibt eine Änderung der inneren Energie als Summe der Wärmezufuhren und -entzüge sowie der verrichteten Arbeit am entsprechenden (geschlossenem) System: und oder auch Innere Energie U und ihre natürlichen Variablen Entropie S, Volumen V und Stoffmenge n sind alles extensive Zustandsgrößen. Die innere Energie ändert sich bei einer Skalierung des thermodynamischen Systems proportional zur entsprechenden Zustandsgröße (S,V). Der Proportionalitätsfaktor ist α. Daraus folgt: mit ni (i = 1,...,K) : Stoffmenge der Teilchen vom Typ i.Solch eine Funktion wird homogene Funktion ersten Grades genannt. Mit dem Euler-Theorem und dem ersten Hauptsatz folgt die Euler-Gleichung für die innere Energie:
kB bezeichnet hier die Boltzmann-Konstante R bezeichnet hier die ideale Gaskonstante
|
| Dieser Artikel basiert auf dem Artikel Innere_Energie aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





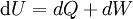
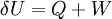
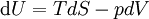
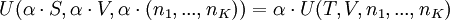
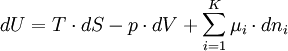
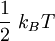 ). Für ein ideales Gas mit drei Freiheitsgraden und
). Für ein ideales Gas mit drei Freiheitsgraden und 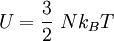 oder für
oder für