Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Mathematische Struktur der QuantenmechanikWeiteres empfehlenswertes Fachwissen
Formulierung durch von NeumannDie wesentlichen Grundlagen für die mathematisch strenge Formulierung der Quantenmechanik wurden im Jahr 1932 durch John von Neumann formuliert. Demnach lässt sich ein physikalisches System allgemein durch drei wesentliche Bestandteile beschreiben: Seine Zustände, seine Observablen und seine Dynamik (d.h. durch seine zeitliche Entwicklung). Postulate der QuantenmechanikDie quantenmechanische Beschreibung eines Systems basiert auf Postulaten, die im folgenden zusammengefasst sind:
Quantenmechanische ZuständeIn der klassischen Mechanik wird der Zustand eines physikalischen Systems mit f Freiheitsgraden und dessen zeitliche Entwicklung durch die Angabe von f Paaren kanonisch konjugierter Variablen qi,pi vollständig bestimmt. Weil in der Quantenmechanik zwei entsprechend zueinander konjugierte Observablen prinzipiell nicht gleichzeitig beliebig genau bestimmbar sind, stellt sich die grundsätzliche Frage, inwiefern eine entsprechende Definition des Zustands eines quantenphysikalischen Systems sinnvoll ist. Der fundamentale Ansatz im Rahmen der Quantenmechanik, dass ein physikalisches System ausschließlich über gleichzeitig messbare Observablen zu definieren ist, ist einer ihrer wesentlichen Unterschiede zur klassischen Mechanik. Erst durch die konsequente Umsetzung einer solchen Zustandsdefinition lässt sich eine Vielzahl quantenphysikalischer Phänomene theoretisch beschreiben. Im Rahmen der Quantenmechanik wird ein physikalischer Zustand
Ein solcher Zustand wird häufig auch reiner Quantenzustand genannt. Er ist über seine zugehörigen Eigenwerte definiert und maximal bestimmt. Es sei betont, dass über einen derart präparierten Quantenzustand – im Gegensatz zum Zustand eines klassischen Systems – nicht sämtliche messbaren Eigenschaften des physikalischen Systems bestimmt sind! Für Observablen, die mit dem VSKO unverträglich sind, kann für jeden ihrer Eigenwerte lediglich eine bestimmte Wahrscheinlichkeit angeben werden, mit der dieser aus einer Messung resultiert; das Messergebnis ist in jedem Fall ein Eigenwert der Observable. Diese prinzipielle Unbestimmtheit hängt mit der o.g. Unbestimmtheitsrelation zusammen. Sie ist eine der wichtigsten Aussagen der Quantenmechanik und ist zugleich Ursache für vielerlei Ablehnung dieser gegenüber. Für ein gegebenes quantenphysikalisches System bilden die zu den Eigenwerten einer Observable gehörenden Eigenzustände einen linearen Zustandsraum kein Eigenzustand der Observable ist. Man spricht in diesem Zusammenhang auch von einer Superposition mehrerer Zustände. Diese Eigenschaft ist vergleichbar mit der von Vektoren in einer Ebene, deren Überlagerung ebenfalls ein Vektor in der Ebene ist. Das einfachste nichttriviale Beispiel eines Quantensystems ist das Zweizustandssystem, welches sich experimentell als sog. Qubit realisieren lässt. Für eine ausführliche quantenmechanische Beschreibung des Zweizustandssystems sei auf den Artikel zum Qubit verwiesen. Statistische Aussagen der Quantenmechanik
Aus der Zerlegung des Zustandes nach den Eigenzuständen Demnach ergeben sich bei wiederholter Durchführung einer Messung einer Observablen i.A. unterschiedliche Messergebnisse, auch wenn das System vor der Messung immer im gleichen Zustand war. Ausnahme: Sofern das System in einem Eigenzustand einer Observablen O präpariert wurde, ergeben weitere Messungen dieser Observablen jeweils den gleichen Messwert. Experimentell lassen sich die statistischen Verteilungen der Messwerte ni durch wiederholte Durchführung von Messungen an identisch präparierten Systemen ermitteln (siehe Abb. 3). Dieser Zusammenhang zwischen dem Messprotokoll und dem mathematischen Kalkül der Quantenmechanik bestätigt sich in allen Experimenten. Zeitliche EntwicklungDie Dynamik von Quantenzuständen wird durch unterschiedliche Modelle, die sog. „Bilder“, beschrieben, welche sich durch Redefinition der Operatoren und Zustände ineinander überführen lassen und somit äquivalent sind. Im sog. Schrödinger-Bild ergibt sich die Dynamik aus folgender Betrachtung:
Der Zustand ist definiert durch eine differenzierbare Abbildung der durch t parametrisierten Zeit auf den Hilbertraum der Zustände. Wenn mit Im Heisenberg-Bild der Quantenmechanik wird anstelle zeitlicher Änderungen der Zustände, die in diesem Bild konstant bleiben, die Zeitabhängigkeit durch zeitabhängige Operatoren für die Observablen beschrieben. Für die zeitabhängigen Heisenberg-Operatoren ergibt sich die Differentialgleichung Es kann gezeigt werden, dass die sich aus dem Schrödinger-Bild und dem Heisenberg-Bild ergebenden Erwartungswerte für die Observable „ Das sogenannte Dirac-Bild oder Wechselwirkungsbild hat sowohl zeitabhängige Zustände als auch zeitabhängige Operatoren, wobei für Zustände und Operatoren unterschiedliche Hamiltonoperatoren gelten. Dieses Bild ist dann am nützlichsten, wenn die zeitliche Entwicklung der Zustände exakt lösbar ist, sodass sämtliche mathematischen Komplikationen auf die Zeitentwicklung der Operatoren begrenzt bleiben. Aus diesem Grund wird der Hamiltonoperator für die Zustände als „freier Hamiltonoperator“ und der Hamiltonoperator für die Observablen als „Wechselwirkungs-Hamiltonian“ bezeichnet. Die dynamische Entwicklung wird durch folgende Gleichungen beschrieben: Das Heisenbergbild entspricht am ehesten dem Modell der klassischen Mechanik, unter pädagogischen Gesichtspunkten gilt jedoch das Schrödingerbild als am einfachsten verständlich. Das Dirac-Bild wird häufig in der Störungstheorie – speziell in der Quantenfeldtheorie – angewandt. Manche Wellenfunktionen bilden Wahrscheinlichkeitsverteilungen, die sich mit der Zeit nicht ändern. Viele Systeme, die in der klassischen Mechanik mit einem dynamischen Zeitverhalten beschrieben werden müssen, weisen in der quantenmechanischen Beschreibung solche „statischen“ Wellenfunktionen auf. Zum Beispiel wird ein einzelnes Elektron in einem Atom im Grundzustand durch eine kreisförmige Trajektorie um den Atomkern beschrieben, während es in der Quantenmechanik durch eine statische, kugelsymmetrische Wellenfunktion beschrieben wird, die den Atomkern umgibt (siehe Bild 1). (Man beachte, dass nur die kleinsten Drehimpuls-Zustände, die „s“-Wellen- kugelsymmetrisch sind). Die Schrödingergleichung ist wie die eng verwandte Heisenberggleichung und die Gleichungen des Wechselwirkungsbildes eine partielle Differentialgleichung, die nur für einige wenige Modellsysteme analytisch gelöst werden kann (zu den wichtigsten Beispielen gehören der quantenmechanische harmonische Oszillator und das Elektron im Coulombpotential). Selbst die Elektronenstruktur des Helium-Atoms, das nur ein Elektron mehr als Wasserstoff aufweist, ist bereits nicht mehr analytisch berechenbar. Es existieren jedoch eine Reihe verschiedener Techniken zur Berechnung von Näherungslösungen. Ein Beispiel ist die Störungstheorie, bei der vorhandene analytische Lösungen vereinfachter Modellsysteme als Ausgangspunkt zur Berechnung komplexerer Modelle verwendet werden. Diese Methode ist insbesondere dann erfolgreich, wenn sich die Wechselwirkungen des komplexen Modells als „kleine“ Störungen des einfachen Modellsystems formulieren lassen. Eine andere Methode ist die sog. „semiklassische Näherung“, die auf Systeme angewendet werden kann, die nur kleine Quanteneffekte aufweisen. Die quantenmechanisch bedingten Effekte können dann unter der Annahme klassischer Bewegungstrajektorien berechnet werden. Dieser Ansatz wird z. B. bei der Erforschung des Quanten-Chaos zugrundegelegt. Neuere FormalismenEin alternativer Ansatz zur Berechnung quantenmechanischer Systeme ist Feynmans Pfadintegral-Formalismus, bei dem eine quantenmechanische Amplitude eine Summe über die Wahrscheinlichkeitsamplituden für alle theoretisch möglichen Pfade eines Teilchens bei seiner Bewegung von einem Ausgangszustand zu einem Zielzustand bildet. Diese Formulierung ist das quantenmechanische Analogon zu dem klassischen Wirkungsprinzip. Erst in neuerer Zeit ist eine allgemeinere mathematische Beschreibung von Observablen durch positiv-operatorwertige Wahrscheinlichkeitsmaße (positive operator valued probability measures, POVM) entstanden, die in der traditionellen Lehrbuchliteratur noch kaum behandelt wird. Operationen auf Quantensystemen werden in der modernen, aber noch wenig bekannten Version der Quantenmechanik durch „completely positive maps“, vollständig positive Abbildungen, sehr umfassend und mathematisch elegant beschrieben. Diese Theorie verallgemeinert sowohl die unitäre Zeitentwicklung als auch die oben beschriebene traditionelle von-Neumannsche Beschreibung der Veränderung eines Quantensystems bei einer Messung. Konzepte, die nur schwer im traditionellen Bild beschrieben werden können, wie z. B. kontinuierlich ablaufende unscharfe Messungen, fügen sich problemlos in diese neuere Beschreibung ein. Literatur
|
|
| Dieser Artikel basiert auf dem Artikel Mathematische_Struktur_der_Quantenmechanik aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





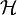 gehörenden Zustandsvektors
gehörenden Zustandsvektors 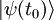 definiert.
definiert.
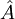 beschrieben. Dieser Operator ist eine Observable.
beschrieben. Dieser Operator ist eine Observable.
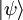 gemessen wird ist die Wahrscheinlichkeit P(an), den nichtentarteten Eigenwert an der entsprechenden Observable
gemessen wird ist die Wahrscheinlichkeit P(an), den nichtentarteten Eigenwert an der entsprechenden Observable 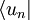 ):
): 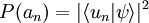 . (Entsprechend bei entartetem und kontinuierlichem Spektrum.)
. (Entsprechend bei entartetem und kontinuierlichem Spektrum.)
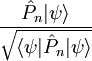 von
von 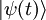 ist gegeben durch die Schrödingergleichung:
ist gegeben durch die Schrödingergleichung:
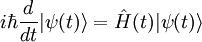 wobei
wobei 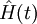 die der totalen Energie des Systems zugeordnete Observable ist.
die der totalen Energie des Systems zugeordnete Observable ist.
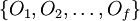 gleichzeitig messbarer Observablen definiert, man spricht in diesem Zusammenhang auch von einem
gleichzeitig messbarer Observablen definiert, man spricht in diesem Zusammenhang auch von einem 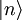 werden als
werden als 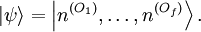
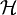 – mathematisch einen sogenannten
– mathematisch einen sogenannten 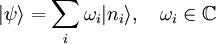
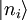 der Observablen ergibt sich mit dem Betragsquadrat
der Observablen ergibt sich mit dem Betragsquadrat 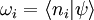
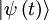 den Zustand des Systems zu einer beliebigen Zeit „t“ beschreibt, gilt die folgende
den Zustand des Systems zu einer beliebigen Zeit „t“ beschreibt, gilt die folgende 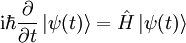
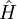 als einem dicht-definierten selbst-adjungierten Operator, dem sog.
als einem dicht-definierten selbst-adjungierten Operator, dem sog. 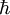 . Als Observable entspricht
. Als Observable entspricht ![\mathrm{i}\hbar{\mathrm{d}\over \mathrm{d}t}\hat A(t) = [\hat A(t),\hat H]](images/math/d/3/0/d309113732286eeeb43c5eddca05445b.png)
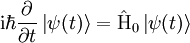
![i\hbar{\partial\over\partial t}\hat A(t) = [\hat A(t),\hat H_{\rm int}]](images/math/8/f/a/8fa6c5fab47ebb0a36de30198d405750.png)


