Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
RollwiderstandDer Rollwiderstand (auch: Rollreibung oder rollende Reibung) entspricht dem Verformungswiderstand eines sich abwälzenden Körpers. Als Kennwert wird der Rollwiderstandskoeffizient cR (auch: Rollwiderstandsbeiwert, Rollreibungsbeiwert usw.) angegeben.
Produkt-Highlight
GrundlagenDie Verformung erfolgt sowohl an dem Wälzkörper selbst als auch an der Wälzkörperbahn und zwar am Berührungspunkt oder an der Berührungslinie. In der Regel ist dies eine elastische Verformung. Ohne diese (meist nicht sichtbare) Verformung ist die Abwälzbewegung nicht möglich. Nach dem Hookeschen Gesetz ist die Verformung proportional der Belastung.
Häufig kommt es infolge der Dauerbelastung zu einer Materialermüdung und Teile werden herausgelöst. Das ist die sogenannte Grübchenbildung (englisch: Pitting). Mathematische BehandlungBeim Abrollen werden sowohl der rollende Körper als auch die Unterlage (die Fahrbahn) verformt. Dadurch wird die Kontaktkraft zwischen Körper und Unterlage asymmetrisch (Fig.1). Der Ersatz der Kontaktkräfte durch statisch äquivalente Einzelkräfte ergibt eine Normalkraft FN, welche um die Strecke d nach vorne verschoben ist, und eine Reibungskraft FR entgegen der Bewegungsrichtung (Fig.2). Beide Kräfte stehen senkrecht zueinander. Aus den Gleichgewichtsbedingungen folgt Die Reibungskraft FR ist direkt vom Radius R des rollenden Körpers abhängig, große Räder rollen also leichter. Im Gegensatz dazu hat bei der Haft- oder der Gleitreibung die Größe der Körper keinen Einfluss. Der Rollwiderstand ist demnach proportional zur Normalkraft. Bei horizontaler Bewegung ist die Normalkraft gleich der Gewichtskraft FG=mg des abrollenden Körpers. In gleicher Weise hängen auch Haft- und Gleitreibung von der Normalkraft ab, nur die Porportionalitätskonstanten sind unterschiedlich. RollwiderstandskoeffizientDas Verhältnis Dann bekommt bekommt der Ausdruck für die Rollreibung FR die Form Der Rollwiderstandskoeffizient cR (veraltet auch: Rollwiderstandsbeiwert, Rollreibungsbeiwert und ähnliches, der Ausdruck „Beiwert“ ist nicht mehr normgemäß) ist eine dimensionslose (einheitenfreie) Zahl, die nur von Materialeigenschaften und Geometrie des abrollenden Körpers und der Fahrbahn abhängt. Typische Zahlenwerte des Rollwiderstandskoeffizienten liegen um ein bis über zwei Größenordnungen unter denen des Gleitreibungskoeffizienten. Typische Rollwiderstandskoeffizienten cR
Grenzen der TheorieDie oben beschriebene Beziehung Extreme Werte für Geschwindigkeiten und Temperaturen sowie eventuell chemische Einflüsse an den Kontaktstellen können mit diesem Modell nicht erfasst werden. Weiterführende Informationen
|
|||||||||||||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Rollwiderstand aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


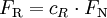 – Rollwiderstand ist Rollwiderstandskoeffizient mal Normalkraft
– Rollwiderstand ist Rollwiderstandskoeffizient mal Normalkraft



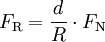
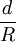 ist materialtypisch. Daher ist es sinnvoll, hierfür einen Koeffizienten zu definieren.
ist materialtypisch. Daher ist es sinnvoll, hierfür einen Koeffizienten zu definieren.
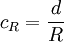
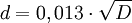 ; d und D in mm. Bei 800 mm Raddurchmesser ergibt sich ca. 0,4 mm, was einem Koeffizienten von 0,001 entspricht.
; d und D in mm. Bei 800 mm Raddurchmesser ergibt sich ca. 0,4 mm, was einem Koeffizienten von 0,001 entspricht.
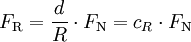 ist ein vereinfachtes Modell, welches für die meisten Berechnungen in der Technik ausreichend ist. Die Abhängigkeit der Reibung von weiteren Größen (Kontaktkraft, Geschwindigkeit, etc.) wird hierbei nicht berücksichtigt.
ist ein vereinfachtes Modell, welches für die meisten Berechnungen in der Technik ausreichend ist. Die Abhängigkeit der Reibung von weiteren Größen (Kontaktkraft, Geschwindigkeit, etc.) wird hierbei nicht berücksichtigt.


