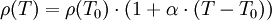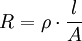Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Spezifischer WiderstandDer spezifische Widerstand (kurz für spezifischer elektrischer Widerstand oder auch Resistivität) ist eine temperaturabhängige Materialkonstante mit dem Formelzeichen ρ (griech. rho). Der elektrische Widerstand eines homogenen elektrischen Leiters lässt sich aus den Werten des Materials errechnen. Die abgeleitete SI-Einheit ist [ρ]SI = Ω · m (gekürzt aus dem anschaulichen Ω · m2 / m). Der Kehrwert des spezifischen Widerstands ist die elektrische Leitfähigkeit. Weiteres empfehlenswertes Fachwissen
UrsacheVerantwortlich für den spezifischen elektrischen Widerstand in reinen Metallen sind Stöße der Ladungsträger (hier Elektronen) mit Gitterschwingungen (Phononen). Dazu kommen noch Anteile durch Verunreinigungen, Fehlstellen und Gitterbaufehler. Der spezifische elektrische Widerstand kann durch einen von der Temperatur abhängigen Anteil des reinen Metalls und einen von der Temperatur unabhängigen Anteil, der von der Störstellen- bzw. Fremdatomkonzentration abhängt, beschrieben werden (Matthiessensche Regel). Bei allen Leitern ändert sich der spezifische Widerstand mit der Temperatur in einem jeweils begrenzten Temperaturbereich näherungsweise linear. wobei α der Temperaturkoeffizient, T die Temperatur und T0 beliebige Temperatur, z. B. T0 = 293,15 K = 20 °C, bei der der spezifische elektrische Widerstand ρ(T0) bekannt ist (siehe Tabelle unten). Je nach Vorzeichen des linearen Temperaturkoeffizienten unterscheidet man zwischen Kaltleiter (engl.: positive temperature coefficient of resistance, PTC) und Heißleiter (engl.: negative temperature coefficient of resistance, NTC). Die lineare Temperaturabhängigkeit gilt nur in einem begrenzten Temperaturintervall. Bei reinen Metallen kann dieser Bereich vergleichsweise groß sein. Darüberhinaus muss man Korrekturen anbringen (Siehe auch: Kaltleiter, Heißleiter, Kondo-Effekt). Starke Abweichungen gibt es auch bei Supraleitern, wobei der Widerstand unterhalb der Sprungtemperatur ganz verschwindet. Der spezifische elektrische Widerstand von Legierungen ist nur gering von der Temperatur abhängig, hier überwiegt der Anteil der Störstellen. Ausgenutzt wird dies beispielsweise bei Konstantan oder Manganin. Berechnung des elektrischen Widerstands von LeiternDer Widerstand eines Leiters mit einem über seine Länge konstanten Querschnitt beträgt: wobei R der elektrische Widerstand, ρ der spezifische Widerstand, l die Länge und A die Fläche des Querschnitts (Schnitt senkrecht zur Längsachse eines Körpers) eines Leiters ist, aber Querschnitt A und Durchmesser d nicht zu verwechseln sind. Die Voraussetzung für die Gültigkeit dieser Formel für den elektrischen Widerstand R ist eine konstante Stromdichteverteilung über den Leiterquerschnitt A, d. h. an jedem Punkt des Leiterquerschnitts ist die Stromdichte J gleich groß. Nährungsweise ist das gegeben, wenn die Länge des Leiters groß im Vergleich zu den Abmessungen seines Querschnitts ist und der Strom „lange genug“ fließt, also bei Gleich- und niederfrequentem Wechselstrom (vgl. Skineffekt). Einteilung von Materialien nach ihrem spezifischen WiderstandDer spezifische Widerstand eines Materials wird häufig für die Einordnung als Leiter, Halbleiter oder Isolator verwendet. Die Unterscheidung erfolgt anhand des spezifischen Widerstands:
Wichtig ist, dass diese Einteilung keine festen Grenzen hat und daher nur als Richtlinie zu betrachten ist. Hauptgrund dafür ist die Temperaturabhängigkeit des elektrischen Widerstands, vor allem bei Halbleitern. Eine Einteilung anhand der Lage des Fermi-Niveaus ist hier sinnvoller.
LiteraturAls Standardwerk für tabellarische Daten zum spezifischen (elektrischen) Widerstand empfiehlt sich:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Spezifischer_Widerstand aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |