Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
SpinDer Spin (von engl. spin, Drehung, Drall) ist eine quantenmechanische Eigenschaft von Elementarteilchen. Obwohl die klassische Vorstellung von einem rotierenden Teilchen nach heutiger und logischer Sichtweise falsch ist, kann dieses Bild doch beim Verständnis helfen. Der Spin verhält sich physikalisch (z. B. unter Rotationen des Raumes) wie der Drehimpuls. Außerdem gilt der Erhaltungssatz für den Gesamtdrehimpuls nur für die Summe aus (klassischem) Bahndrehimpuls und Spin eines Systems. Daher ist der Spin im Gegensatz zum Isospin nicht nur eine dem Drehimpuls (mathematisch) analoge Eigenschaft, sondern tatsächlich eine Art von Drehimpuls. Relativistisch (d. h. innerhalb der vierdimensionalen Raumzeit) wird Spin mithilfe von Spinoren beschrieben. Weiteres empfehlenswertes Fachwissen
Spin, Spinquantenzahl und SpineigenzustandEin in der Quantenmechanik durch seine Wellenfunktion (d. h. den Zustandsvektor) Ψ gegebenes Objekt wird bei einer (idealen) Messung in einen Eigenzustand mit assoziiertem Eigenwert geworfen, die Eigenwerte sind die möglichen Messwerte. Die Spineigenzustände und -eigenwerte ergeben sich - in Analogie zum quantenmechanischen Drehimpuls - aus den Lösungen der folgenden Eigenwertgleichungen: Dabei sind Die Spinquantenzahl s eines Elementarteilchens ist fest vorgegeben und kann sich nicht ändern. Die möglichen sz-Werte ergeben sich dann zu Das heißt, dass ein Spin-0-Teilchen nur einen Eigenwert Die Zustände des Spins werden durch 2s+1-komponentige Spinoren dargestellt. Statt im Spinorraum wird aber meistens im Spinraum gerechnet. Ein Spinor lässt sich nach den Basisvektoren des Spinraumes entwickeln: Im Spinraum werden die Spinoperatoren durch Matrizen und die Zustände durch Vektoren dargestellt. Da diese Eigenschaft genannt Spin nur eine stark begrenzte Zahl von Zuständen annehmen kann, kann es sich logischerweise nicht um eine Eigenrotation der Teilchen handeln, wie bei der ursprünglichen Idee. Es gäbe keine Erklärung für bestimmte Rotationsgeschwindigkeiten und identische Orientierung der Rotationsachsen aller Teilchen der gleichen Art. Spin als ErhaltungsgrößeDie Spinquantenzahl s eines Elementarteilchens ist unveränderlich, die Spinausrichtung allerdings nicht. Auch der Gesamtspin eines Systems aus mehreren Teilchen ist keine Erhaltungsgröße, jedoch sein Gesamtdrehimpuls. Wenn also Reaktionen etwa in der Atomphysik beobachtet werden, dann ist die Summe aller Drehimpulseigenwerte vor und nach der Reaktion die gleiche. Die für die Erhaltungsgröße "Spin" verantwortliche Symmetrie ist beschrieben durch die eigentliche Lorentz-Gruppe SO(3,1). So gesehen ist der Spin eine Erhaltungsgröße relativistischer Theorien. Der kompakte Anteil der speziellen orthochronen Lorentzgruppe ist isomorph zu SU(2) x SU(2). Diese Tatsache rechtfertigt die in der Physik übliche Systematik der verwendeten Darstellungen für relativistische Wellenfunktionen, die sich dann mit den beiden Eigenwerten j1 und j2 der SU(2) adressieren lassen:
Spin und Magnetisches MomentDer Spin eines Elementarteilchens kann über das mit ihm assoziierte magnetische Moment gemessen werden (Einstein-de-Haas-Effekt, Stern-Gerlach-Experiment). Über dieses magnetische Moment tritt der Spin in Wechselwirkung mit magnetischen Feldern, so dass ein Teilchen je nach Ausrichtung seines Spin in einem Magnetfeld unterschiedliche Energiemengen enthält. Im Atom treten auf diese Weise Wechselwirkungen zwischen Elektron und Atomkern oder zwischen verschiedenen Elektronen auf. Diese Wechselwirkung wird technisch in der Kernspinresonanz (z. B. im Kernspintomografen) bzw. in der Elektronenspinresonanz ausgenutzt. Spin und StatistikGemäß dem Standardmodell der Physik gruppiert man Elementarteilchen nach ihrem Spin in Bosonen (ganzzahliger Spin) und Fermionen (halbzahliger Spin). Die Zuteilung "halb-" bzw. "ganzzahliger Spin" zur jeweiligen Teilchenart wird durch das Spin-Statistik-Theorem begründet. Bosonen und Fermionen haben ein unterschiedliches Symmetrieverhalten unter Rotationen: Die Wellenfunktion eines Bosons geht unter einer Rotation von 360 Grad in sich selbst über. Bei einem Fermion entsteht bei einer Rotation um 360 Grad jedoch nicht die identische Wellenfunktion, sondern − Ψ. Erst bei einer Rotation um 720 Grad ergibt sich Ψ. Dies ist der letztendliche Grund, dass für Fermionen das Pauli-Prinzip gilt. Vertauscht man zwei Fermionen, negiert sich das Vorzeichen der Gesamtwellenfunktion des Systems, während die Vertauschung zweier Bosonen die Wellenfunktion unbeeinflusst lässt. Die Folge ist, dass sich zwei Fermionen nie im selben Zustand aufhalten können, zwei Bosonen hingegen schon. Dem Spin-Statistik-Theorem zufolge gehorchen alle Fermionen der Fermi-Dirac-Statistik, alle Bosonen der Bose-Einstein-Statistik. Aufgrund dieser Eigenschaften und der Ununterscheidbarkeit von Elementarteilchen können nur immer zwei Fermionen ein Energieniveau besetzen, nämlich eines mit Spin-Up und eines mit Spin-Down. Diese Gesetzmäßigkeit ist als das Pauli-Prinzip bekannt. Dagegen können beliebig viele Bosonen einen Energiezustand besetzen (Bose-Einstein-Kondensat). Spin, Praktische BedeutungWie im vorherigen Abschnitt dargestellt, sind alle Elementarteilchen entweder Fermionen oder Bosonen – je nach Spin. Insbesondere sind Elektronen Fermionen. Daher kann in einem Atom immer nur ein Elektron einen Zustand besetzen (siehe Pauli-Prinzip, die Elektronen müssen sich in einem Orbital wenigstens durch den Spin (+1/2 oder -1/2) unterscheiden). So kommt es zur Bildung der uns bekannten Materie. Wären Elektronen Bosonen, so würden sie alle das unterste Energieniveau im Atom besetzen. Die uns bekannte Materie und insbesondere die Verbindung von Atomen zu Molekülen würde nicht existieren. Daher ist der Spin eine der wichtigsten Eigenschaften der Materie zusammen mit der elektrischen Ladung und der Masse. Eine direkte praktische Anwendung des Spins von Atomkernen ist die Magnetresonanztomographie. GeschichteIm Zusammenhang mit der Messung von Emissionsspektren von Alkalimetallen wurde der Spin erstmals bemerkt, nämlich durch die Aufspaltung von Spektrallinien in zwei benachbarte Teillinien. Wolfgang Pauli schlug 1924 einen quantenmechanischen Freiheitsgrad, der zwei Werte annehmen kann, für das Elektron vor. Hierdurch konnte er die Aufspaltung der Linien erklären und begründen, dass genau zwei Elektronen sich ein Atomorbital teilen (siehe auch Atommodell). Ralph Kronig, ein Assistent Alfred Landés, schlug 1925 vor, dieser unbekannte Freiheitsgrad werde von der Eigenrotation des Elektrons hervorgerufen. Aufgrund der Kritik Paulis an dieser Idee blieb Kronigs Vorschlag unveröffentlicht. Ebenfalls 1925 postulierten Samuel Abraham Goudsmit und George Eugene Uhlenbeck den Elektronenspin zur Erklärung der Linienaufspaltung in den Spektren wasserstoffartiger Atome (z. B. der Natrium-D-Linie) sowie des anomalen Zeeman-Effekts. Im Jahre 1927 formulierte Pauli eine Quantentheorie des Spins für das Elektron. Mit Hilfe der Pauli-Matrizen konnte er Elektronen-Wellenfunktionen als 2-komponentige Spinoren darstellen. 1928 stellte Paul Dirac eine relativistische Bewegungsgleichung für das Elektron auf. Die Dirac-Gleichung beschreibt den halbzahligen Spin und sagte auch ein Antiteilchen des Elektrons voraus, das später nachgewiesene Positron. Siehe auch |
|||||||||||||
| Dieser Artikel basiert auf dem Artikel Spin aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





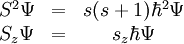
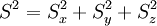 und
und 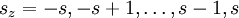
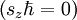 bzgl. Sz besitzt. Ein Spin-1/2-Teilchen hat zwei Eigenwerte
bzgl. Sz besitzt. Ein Spin-1/2-Teilchen hat zwei Eigenwerte 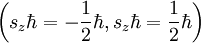 und allgemein hat ein Spin-s-Teilchen 2s+1 Eigenwerte bzgl. Sz.
und allgemein hat ein Spin-s-Teilchen 2s+1 Eigenwerte bzgl. Sz.