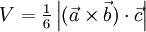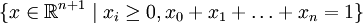Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Tetraeder
Das Wort wird jedoch nur selten in dieser allgemeinen Bedeutung gebraucht. Meist ist mit Tetraeder das regelmäßige (oder gleichseitige) Tetraeder gemeint, während das allgemeine Tetraeder als dreiseitige Pyramide oder dreidimensionaler Simplex bezeichnet wird. Weiteres empfehlenswertes Fachwissen
Regelmäßiges TetraederDas (oft auch: der) regelmäßige Tetraeder (reguläre Tetraeder) ist einer der fünf platonischen Körper, genauer: ein (dreidimensionales) Polyeder (ein Vielflächner) mit
Das Tetraeder ist auch eine gleichseitige dreiseitige Pyramide (mit einem gleichseitigen Dreieck als Grundfläche). Symmetrie
Wegen seiner hohen Symmetrie – alle Ecken, Kanten und Flächen sind untereinander gleichartig – ist das Tetraeder ein reguläres Polytop. Es hat
Insgesamt hat die Symmetriegruppe des Tetraeders – die Tetraedergruppe – 24 Elemente. Sie ist die symmetrische Gruppe S4 und bewirkt alle 4! = 24 Permutationen der Ecken bzw. der Seitenflächen. Sie ist Untergruppe der Oktaedergruppe (Würfelgruppe). Im Einzelnen gehören zur Tetraedergruppe
sowie
Die geraden Permutationen bilden eine Untergruppe der Tetraedergruppe, die so genannte alternierende Gruppe A4. Manchmal wird der Begriff Tetraedergruppe auch nur für diese unter Ausschluss der Spiegelungen verwendet. Weitere EigenschaftenVerhältnis zu Oktaeder, Würfel, archimedischen Körpern
Durch Verbinden der Flächenmittelpunkte erhält man wieder ein Tetraeder. Man sagt deshalb: Das Tetraeder ist zu sich selbst dual. Die Seitenlänge des neuen Tetraeders beträgt ein Drittel der ursprünglichen Seitenlänge. Mit Hilfe dieser beiden Tetraeder können Körper konstruiert werden, die ebenfalls die Tetraedergruppe als Symmetriegruppe haben. So erhält man zum Beispiel
(Siehe dazu auch das Beispiel weiter unten.) Umgebender Würfel
Das Tetraeder kann in einen Würfel so einbeschrieben werden, dass seine Ecken zugleich Würfelecken und seine sechs Kanten Diagonalen der Würfelflächen sind. (Die acht Ecken des Würfels bilden zwei disjunkte Mengen von je vier Ecken, die den beiden möglichen Lagen des Tetraeders entsprechen.) Das Volumen dieses Würfels ist das Dreifache des Tetraedervolumens. Dual dazu kann das Tetraeder einem Oktaeder so umbeschrieben werden, dass vier der Oktaederflächen in den Begrenzungsflächen des Tetraeders liegen und die sechs Ecken des Oktaeders die Mittelpunkte der sechs Tetraederkanten sind. (Die acht Flächen des Oktaeders bilden zwei disjunkte Mengen, die den beiden Lagen für das dem Oktaeder umbeschriebene Tetraeder entsprechen.) Winkel
Der Winkel zwischen zwei Begrenzungsflächen des regelmäßigen Tetraeders (in der Zeichnung mit α bezeichnet) beträgt 70,53° (Rundungsgenauigkeit wie bei den nachfolgenden Angaben zwei Nachkommastellen). Jede Kante bildet mit der gegenüberliegenden Fläche einen Winkel (β) von 54,74°. Die Verbindungsstrecken zwischen dem Tetraedermittelpunkt und zwei Ecken schließen jeweils einen Winkel von Zur Berechnung des Tetraederwinkels Artikel Stumpfer Winkel. QuerschnittDas regelmäßige Tetraeder kann so in zwei Teile geschnitten werden, dass die Schnittfläche ein Quadrat ist. Die Teile sind kongruent zueinander. Liegt die Schnittebene durch ein regelmäßiges Tetraeder parallel zu einer der vier Seitenflächen, dann ergibt der Querschnitt ein gleichseitiges Dreieck. Liegt die Schnittebene durch ein regelmäßiges Tetraeder parallel zu zwei gegenüberliegenden Kanten, dann ergibt der Querschnitt ein Rechteck. Hat die Schnittebene zusätzlich noch von diesen beiden Kanten den gleichen Abstand, also teilt sie die übrigen vier Kanten genau zur Hälfte, dann ist das Schnittbild ein Quadrat. Das Quadrat hat eine Kantenlänge, die genau halb so lang ist, wie die Länge einer Kante des Tetraeders. BeispielDie Einbettung des Tetraeders in einen Würfel bietet eine einfache Möglichkeit, ein regelmäßiges Tetraeder zu konstruieren. Bezeichnen wir die Eckpunkte des Würfels an der Basis mit A, B, C und D sowie die darüberliegenden Eckpunkte mit E, F, G und H, so bilden A, C, F und H sowie B, D, E und G jeweils die Ecken eines Tetraeders. Betrachtet man z. B. in einem räumlichen kartesischen Koordinatensystem den Würfel, dessen Ecken die Koordinaten +1 und -1 haben, so erhält man für das erste Tetraeder die Ecken
Die Kanten sind: AC, AF, AH, CF, CH und FH. Die Seitenflächen sind die Dreiecke ACF, ACH, AFH und CFH. Das zweite Tetraeder hat die Ecken
Der Durchschnitt dieser beiden Tetraeder ist das von den Punkten (1,0,0), (-1,0,0), (0,1,0) (0,-1,0), (0,0,1) und (0,0,-1) bestimmte Oktaeder. Ihre Vereinigung ist ein Sternkörper mit 8 Spitzen (in jeder Ecke des Würfels eine). Seine konvexe Hülle ist daher der Würfel. Formeln
AnwendungenObwohl das Tetraeder nicht Stein einer Parkettierung des Raumes ist, tritt es (siehe oben) im kubischen Kristallsystem auf. In der Chemie spielt das Tetraeder bei der räumlichen Anordnung von Atomen in Verbindungen eine große Rolle. So sind beispielsweise die Kohlenstoffatome im Diamantgitter tetraedisch angeordnet, jedes Atom ist von vier weiteren Atomen umgeben. Auch das Methan bildet, aufgrund der sp3-Hybridisierung des Kohlenstoff-Atoms, ein Tetraeder. Auch die Form der Tetrapoden, die an Küsten als Wellenbrecher eingesetzt werden, leitet sich vom Tetraeder ab. Allgemeines Tetraeder (dreidimensionaler Simplex)Ein Tetraeder im allgemeinen Sinn, also ein Körper mit vier Seitenflächen, ist immer eine dreiseitige Pyramide, also mit einem Dreieck als Grundfläche und drei Dreiecken als Seitenflächen, und hat daher auch vier Ecken sowie sechs Kanten. Da er die für einen Körper im Raum kleinste mögliche Zahl von Ecken und Seiten hat, wird er in der Fachsprache (dreidimensionaler) Simplex genannt. Die zweidimensionalen Simplizes sind die Dreiecke.
Im Analogien in höheren DimensionenDie Analoga des Tetraeders in beliebiger Dimension n werden als (n-dimensionale) gleichseitige Simplexe bezeichnet und sind ebenfalls reguläre Polytope. Der n-dimensionale Simplex hat n + 1 Ecken und wird von n + 1 (n-1)-dimensionalen Simplexen (als Facetten) begrenzt. Der vierdimensionale Simplex hat 5 Ecken, 10 gleichlange Kanten, 10 gleichseitige Dreiecke als Seitenflächen und 5 dreidimensionale Tetraeder als Facetten. Ein nulldimensionaler Simplex ist ein Punkt, ein eindimensionaler Simplex ist eine Strecke, ein zweidimensionaler Simplex ist ein Dreieck. In Koordinaten kann man ein reguläres n-Simplex beispielsweise durch beschreiben. Beispielsweise kann sich für n = 2 ein gleichseitiges Dreieck ergeben, das von den Punkten (1,0,0),(0,1,0),(0,0,1) im dreidimensionalen Raum aufgespannt wird. |
||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Tetraeder aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. | ||||||||||||||||





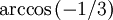 ein, dies entspricht 109,47°. Der zuletzt genannte Winkel (
ein, dies entspricht 109,47°. Der zuletzt genannte Winkel (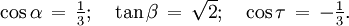
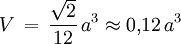
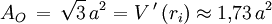
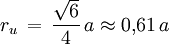
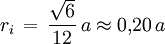
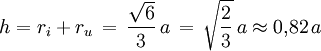
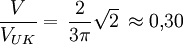
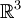 kann ein Tetraeder auch durch einen Punkt und den drei Vektoren zu den angrenzenden Punkten beschrieben werden. Bezeichnet man diese Vektoren mit
kann ein Tetraeder auch durch einen Punkt und den drei Vektoren zu den angrenzenden Punkten beschrieben werden. Bezeichnet man diese Vektoren mit 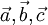 , so berechnet sich das Volumen des Tetraeders mit
, so berechnet sich das Volumen des Tetraeders mit