Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Volumenarbeit
Die Volumenarbeit oder auch Volumenänderungsarbeit ist die an einem geschlossenen System zu leistende Arbeit (in der Abbildung rechts ist dies die Arbeit, die der Kolben an dem im Zylinder enthaltenen Gas verrichtet), um das Volumen V1 auf das Volumen V2 zu komprimieren (V1 > V2) oder durch Expansion (V1 < V2) zu vergrößern. Im ersten Fall muss dabei Arbeit geleistet werden, im zweiten Fall wird Arbeit, d. h. Energie, frei.
Hierbei ist F(s) die Kraft, die längs eines Weges s wirkt. Das Minuszeichen ist Konvention. So erreicht man, dass zugeführte Arbeit positiv ist (ds < 0), freiwerdende Energie dagegen ein negatives Vorzeichen erhält. Weiteres empfehlenswertes Fachwissen
Vorgang ohne ReibungBei der reversibel, d. h. reibungsfrei und quasistatisch zugeführten Arbeit ist in dem dargestellten Zylinder mit dem Querschnitt A wegen
Reibungsbehafteter VorgangNimmt man den realen Fall, dass zwischen dem Kolben und dem Zylinder eine Reibungskraft wirkt, so muss beim Komprimieren zusätzlich zur Volumenänderungsarbeit die Reibungsarbeit aufgebracht werden. Diese erhöht, wenn sie nicht durch Kühlung als Wärme nach außen abgeführt wird, die innere Energie des Systems und damit den Druck gegenüber dem reibungsfreien Vorgang. Die Zustandsänderung verläuft vom Punkt 1 zum Punkt 2´. Das heißt also, dass auch die Volumenänderungsarbeit, die der Fläche unter dem Verlauf im p-V-Diagramm entspricht, größer wird, ohne dass darin die Reibungsarbeit selbst enthalten ist. Die von außen aufzubringende Arbeit ist also die Summe aus der nunmehr größeren Volumenänderungsarbeit und der Reibungsarbeit. Einfaches Beispiel zur BerechnungEs sei eine isotherme Verdichtung eines idealen Gases angenommen. Es gilt die Zustandsgleichung
wobei m die Masse ist, R die spezifische Gaskonstante und T die absolute Temperatur. Ist die Temperatur konstant (isotherme Zustandsänderung), lässt sich durch Einsetzen dieser Gleichung das Integral lösen und man erhält:
einsetzen, wobei n die Molmenge ist und Rmol die molare oder allgemeine Gaskonstante. Anhand dieser Gleichung sieht man nun auch, dass bei der Expansion eines idealen Gases die Volumenarbeit negativ ist, also Energie frei wird und im umgekehrten Fall Arbeit geleistet werden muss. Dies folgt aus dem Logarithmus, der für Zahlen kleiner 1 negativ und für Zahlen größer eins positiv ist. LiteraturSiehe auch |
|
| Dieser Artikel basiert auf dem Artikel Volumenarbeit aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


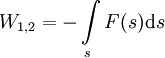 .
.



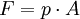 und
und 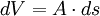
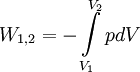 .
.
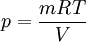
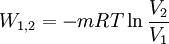
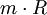 kann man auch
kann man auch