Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Wärmekapazität
Dabei ist es von Nöten, dass der Prozess der Erwärmung quasi-statisch, das heißt sehr langsam erfolgt, so dass während des Prozesses irreversible Erscheinungen keine wesentliche Rolle spielen. Präziser sollte man deshalb von der Gleichgewichtswärmekapazität sprechen. Im Allgemeinen spielen die äußeren Bedingungen, unter denen der Körper erwärmt wird, wie konstanter Druck oder konstantes Volumen, eine Rolle. Bei konstantem Druck wird beispielsweise gleichzeitig Arbeit in Form der thermischen Ausdehnung des Körpers geleistet, was auf Grund der Energieerhaltung zu einer größeren Wärmeaufnahme pro Temperatureinheit führt. Man unterscheidet deshalb die Wärmekapazität für ein konstantes Volumen CV und für einen konstanten Druck Cp. Ist der Körper physikalisch homogen, so ist es sinnvoll, die Wärmekapazität pro Masseneinheit (oder Stoffeinheit) anzugeben, welche dann als spezifische Wärmekapazität (beim Bezug auf 1 kg eines Stoffs) oder Molwärme bzw. molare Wärmekapazität (beim Bezug auf 1 mol eines Stoffs) bezeichnet wird. Erstere wird mit dem Formelsymbol c abgekürzt. Die physikalische Einheit der Wärmekapazität ergibt sich aus ihrer Definition als [J/K], die der spezifischen Wärmekapazität je nach bezogener Stoffeinheit als [J/(K·kg)] oder [J/(K·mol)]. Auch die Temperatur des Stoffes hat einen Einfluss darauf, Beispiel:
Für feste Stoffe kann man in kleinen Temperaturbereichen eine mittlere spezifische Wärmekapazität verwenden. Weiteres empfehlenswertes Fachwissen
Allgemeine BeziehungenZwischen den Wärmekapazitäten bei konstantem Druck Cp und bei konstantem Volumen CV bestehen folgende allgemeine Beziehungen: Hierbei ist
Spezifische Wärmekapazität idealer GaseDie spezifische Wärmekapazität idealer Gase hängt nur von der Temperatur ab und ist von Druck unabhängig. Aus der idealen Gasgleichung folgt: wobei Beispiel (Wasserstoff (H2) bei 20 °C und 1,013 bar)
Die Differenz Um die Wärmekapazität idealer Gase zu überschlagen, gibt es die Möglichkeit, sie über die Freiheitsgrade zu berechnen. Jedes Atom hat drei Freiheitsgrade, die Translationen in den drei Raumdimensionen. Für einatomige Gase gilt:
Für mehratomige Gase gilt:
d. h. je nach Translations-, Rotationsfreiheitsgraden einhalb RS, für die Vibrationsfreiheitsgrade einmal RS. Dabei ist zu beachten, dass bei Raumtemperatur Rotationsfreiheitsgrade üblicherweise angeregt sind (IR-Spektrum), Vibrationsfreiheitsgrade häufig nur zu einem geringen Anteil (UV-Spektrum). Beispiel H2:
Sollte der Isentropenexponent des Idealen Gases bekannt sein, so lassen sich die Wärmekapazitäten aus der Kombination von Formel 1 und der Formel berechnen. Temperaturabhängigkeit der Wärmekapazität eines kristallinen Festkörpers
Bei hohen Temperaturen gilt die Dulong-Petit'sche Regel, die eine konstante molare Wärmekapazität von C = 3R für den Festkörper vorhersagt. Bei niedrigen Temperaturen versagt dieses Modell. In diesem Bereich sagt das Debye-Modell eine T3-Abhängigkeit der Wärmekapazität vorher. Nach dem Debye-Modell wird die molare Wärmekapazität in Abhängigkeit von der Temperatur durch nur eine Stoffgröße, die sogenannte Debye-Temperatur ΘD, bestimmt:
Negative Kapazität (Sterne)Die meisten physikalischen Systeme zeigen eine positive Wärmekapazität. Auch wenn das Gegenteil zunächst absurd erscheint, können Systeme auch eine negative Wärmekapazität aufweisen. Dazu zählen gravitierende Objekte wie zum Beispiel kollabierende Sterne, die sich beim Zusammenziehen (innere Energie verringert sich) erhitzen, oder sehr kleine Systeme (Cluster) aus einigen hundert Atomen nahe an einer Phasenumwandlung. Diese merkwürdige Eigenschaft steht im Zusammenhang mit der thermodynamischen Stabilität. Nur Systeme mit einer positiven Wärmekapazität können im thermodynamischen Sinne als stabil und diese damit auch als extensive Größe betrachtet werden. |
|||||||||||||||
| Dieser Artikel basiert auf dem Artikel Wärmekapazität aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


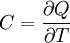
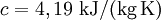
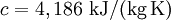



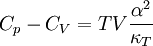
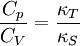
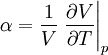 der
der 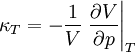 die isotherme Kompressibilität,
die isotherme Kompressibilität, 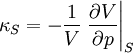 die isentrope Kompressibilität und
die isentrope Kompressibilität und 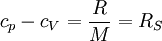
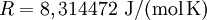 die
die 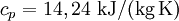
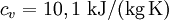
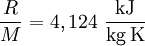
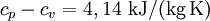 statt
statt 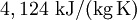 ) erklärt sich daraus, dass Wasserstoff kein hundertprozentig ideales Gas ist.
) erklärt sich daraus, dass Wasserstoff kein hundertprozentig ideales Gas ist.
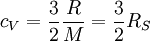 , also
, also 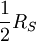 pro Freiheitsgrad.
pro Freiheitsgrad.
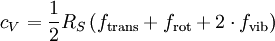 ,
,
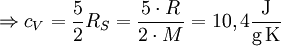 , ohne Vibrationen
, ohne Vibrationen
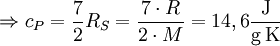 , mit Vibrationen
, mit Vibrationen