Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Wiensches VerschiebungsgesetzDas nach Wilhelm Wien benannte wiensche Verschiebungsgesetz gibt an, bei welcher Wellenlänge λmax bzw. Frequenz νmax ein nach dem planckschen Strahlungsgesetz strahlender Schwarzer Körper je nach seiner Temperatur die größte Strahlungsleistung oder die größte Photonenrate abgibt. Weiteres empfehlenswertes Fachwissen
AllgemeinesDie von einem Schwarzen Körper abgegebene Wärmestrahlung ist ein Gemisch elektromagnetischer Wellen aus einem breiten Wellenlängenbereich. Die Verteilung der Strahlungsintensität auf die einzelnen Wellenlängen wird durch das plancksche Strahlungsgesetz beschrieben. Sie weist ein deutliches Maximum auf, dessen Lage mit dem wienschen Verschiebungsgesetz berechnet werden kann. Insbesondere gilt: Je höher die Temperatur eines Körpers ist, desto kürzer ist die Wellenlänge, bei der das Intensitätsmaximum ausgesandt wird. Daher gibt zum Beispiel Stahl bei Raumtemperatur unsichtbares infrarotes Licht als „Wärmestrahlung“ ab, warmer glühender Stahl leuchtet dunkelrot, heißer flüssiger Stahl glüht fast weiß. Die gebräuchlichste Formulierung des Verschiebungsgesetzes lautet:
Es lassen sich auch Formulierungen des Gesetzes für die Frequenz maximaler Intensität, νmax, sowie für Wellenlänge und Frequenz mit maximaler Photonenrate herleiten. Es ist jeweils zu beachten, dass νmax sich nicht ergibt, indem λmax einfach in die entsprechende Frequenz umgerechnet wird; es liegt an einer anderen Stelle im Spektrum (mit anderen Worten: es gibt kein „objektives“ Maximum). Maximale StrahlungsleistungWellenlängendarstellungDie spektrale spezifische Ausstrahlung eines Schwarzen Körpers der Temperatur T wird durch das plancksche Strahlungsgesetz beschrieben und lautet in der Wellenlängendarstellung: 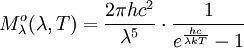 . .
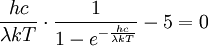 . .Die Substitution 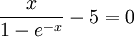 . .Die numerische Lösung ergibt 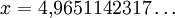 [1], [1],und die Rücksubstitution führt auf das wiensche Verschiebungsgesetz in der Wellenlängendarstellung:
Die Wellenlänge maximaler Strahlungsleistung verschiebt sich also bei einer Temperaturänderung einfach umgekehrt proportional zur absoluten Temperatur des Schwarzen Strahlers: verdoppelt sich die Temperatur des Strahlers, so tritt die größte Strahlungsleistung bei der halben Wellenlänge auf. Die Konstante Die spektrale spezifische Ausstrahlung des Maximums ist proportional zu T5: 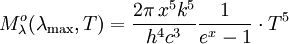 .[3] .[3]FrequenzdarstellungIn der Frequenzdarstellung ist die spektrale spezifische Ausstrahlung gegeben durch 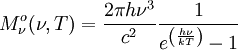 . .Nullsetzen der Ableitung nach ν liefert: 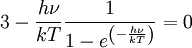 . .Die Substitution Die numerische Lösung ergibt 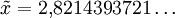 [1], [1],und Rücksubstitution führt auf das wiensche Verschiebungsgesetz in der Frequenzdarstellung:
Die Frequenz maximaler Strahlungsleistung verschiebt sich also proportional zur absoluten Temperatur des Strahlers. Der gemäß CODATA 2006 empfohlene Wert der wienschen Konstanten in der Frequenzdarstellung beträgt Die spektrale spezifische Ausstrahlung des Maximums ist proportional zu T3: 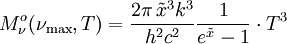 .[3] .[3]Unterschiedliche Maxima in beiden DarstellungenMan beachte, dass wegen der nichtlinearen Umrechnung zwischen Wellenlängen- und Frequenzintervallen nicht die folgende Gleichung: 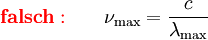 sondern folgende Gleichung gilt: 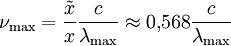 . .
Trägt man das Diagramm einmal gegen eine lineare Frequenzachse und einmal gegen eine lineare Wellenlängenachse auf, so ist auch optisch erkennbar, wie sich die Punkte in jeweils unterschiedlichen Bereichen der Achse zusammendrängen. Es gibt kein „objektives“ Maximum. Maximale PhotonenrateWellenlängendarstellungDie spektrale spezifische Ausstrahlung, ausgedrückt durch die Abstrahlungsrate der Photonen, ist in der Wellenlängendarstellung gegeben durch 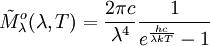 . .Nullsetzen der Ableitung nach ν liefert: 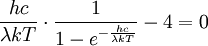 . .Die Substitution Die numerische Lösung ergibt 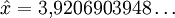 [1], [1],und Rücksubstitution führt auf das wiensche Verschiebungsgesetz für die Photonenrate in der Wellenlängendarstellung:
Die spektrale Photonenrate des Maximums ist proportional zu T4. FrequenzdarstellungIn der Frequenzdarstellung ist die spektrale spezifische Ausstrahlung, ausgedrückt durch die Abstrahlungsrate der Photonen, gegeben durch
Nullsetzen der Ableitung nach ν liefert: 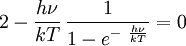 . .Die Substitution Die numerische Lösung ergibt 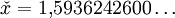 [1], [1],und Rücksubstitution führt auf das wiensche Verschiebungsgesetz für die Photonenrate in der Frequenzdarstellung:
Die spektrale Photonenrate des Maximums ist proportional zu T2. AnwendungsbeispieleNimmt man für die Sonne Glutfarben geben Aufschluss über die Temperatur heißer (über ca. 500 °C) Materialien. Andere Beispiele sind die strahlende Erdoberfläche und die Treibhausgase. Bei den Temperaturen im Bereich von 0° C liegt das Strahlungsmaximum im infraroten Bereich um 10 μm. Bei den Treibhausgasen kommt dazu, daß sie nur teilweise (selektive) schwarze Körper sind. Siehe auchAndere die Strahlung des Schwarzen Körpers betreffende Gesetze sind das plancksche Strahlungsgesetz, das Stefan-Boltzmann-Gesetz, das wiensche Strahlungsgesetz und das Rayleigh-Jeans-Gesetz. Näherungsweise gelten diese Gesetze oft auch für die von nicht-schwarzen Strahlern abgegebene Wärmestrahlung. Quellen
Kategorien: Atomphysik | Thermodynamik |
||||||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Wiensches_Verschiebungsgesetz aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





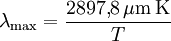
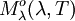
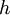
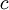
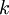
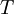
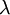
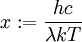 vereinfacht den Ausdruck zu
vereinfacht den Ausdruck zu
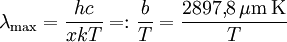
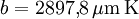 wird auch als wiensche Verschiebungskonstante bezeichnet. Der gemäß CODATA 2006 empfohlene Wert beträgt
wird auch als wiensche Verschiebungskonstante bezeichnet. Der gemäß CODATA 2006 empfohlene Wert beträgt 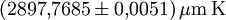 .
.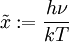 vereinfacht den Ausdruck zu
vereinfacht den Ausdruck zu 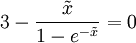 .
.
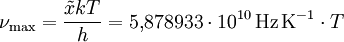
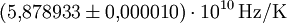 .
.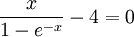 .
.
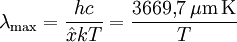
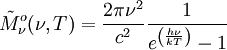 .
.
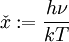 vereinfacht den Ausdruck zu
vereinfacht den Ausdruck zu 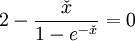 .
.
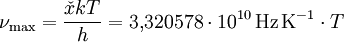
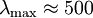 nm an und betrachtet sie näherungsweise als Schwarzen Strahler, so ergibt sich nach dem wienschen Verschiebungsgesetz ihre Oberflächentemperatur zu ca. 5800
nm an und betrachtet sie näherungsweise als Schwarzen Strahler, so ergibt sich nach dem wienschen Verschiebungsgesetz ihre Oberflächentemperatur zu ca. 5800 

