Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Stefan-Boltzmann-GesetzDas Stefan-Boltzmann-Gesetz ist ein physikalisches Gesetz, das die von einem Schwarzen Körper thermisch abgestrahlte Leistung in Abhängigkeit von seiner Temperatur angibt. Es ist benannt nach den Physikern Josef Stefan und Ludwig Boltzmann. Produkt-Highlight
Stefan-Boltzmann-GesetzJeder Körper, dessen Temperatur über dem absoluten Nullpunkt liegt, sendet Wärmestrahlung aus. Ein Schwarzer Körper ist ein idealisierter Körper, der alle auf ihn treffende Strahlung vollständig absorbieren kann (Absorptionsgrad = 1). Nach dem kirchhoffschen Strahlungsgesetz erreicht daher auch sein Emissionsgrad ε den Wert 1, und er sendet die bei der betreffenden Temperatur maximal mögliche thermische Leistung aus. Das Stefan-Boltzmann-Gesetz gibt an, welche Strahlungsleistung P ein Schwarzer Körper der Fläche A und der absoluten Temperatur T emittiert. Es ist mit der Stefan-Boltzmann-Konstanten σ. Die Strahlungsleistung eines Schwarzen Körpers ist also proportional zur vierten Potenz seiner absoluten Temperatur: eine Verdopplung der Temperatur bewirkt, dass die abgestrahlte Leistung um den Faktor 16 ansteigt. Die Stefan-Boltzmann-Konstante ist eine Naturkonstante und ihr Zahlenwert beträgt gemäß CODATA 2000
Dabei sind k die (nicht mit σ zu verwechselnde) Boltzmann-Konstante, h das plancksche Wirkungsquantum und c die Lichtgeschwindigkeit. HerleitungZur Herleitung geht man von der spektralen Strahldichte eines Schwarzen Körpers aus und integriert diese sowohl über den gesamten Halbraum, in den das betrachtete Flächenelement abstrahlt, als auch über alle Frequenzen.
Der Kosinusfaktor berücksichtigt dabei den Umstand, dass bei Abstrahlung in eine beliebige durch die Winkel β und Da der Schwarze Körper grundsätzlich ein diffuser Strahler und seine spektrale Strahldichte daher richtungsunabhängig ist, ergibt das Integral, ausgeführt über den Halbraum, den Wert π. Für die Integration über die Frequenzen ist zu beachten, dass
Integriert man die so erhaltene spezifische Ausstrahlung Mo(T) noch über die abstrahlende Fläche, erhält man das Stefan-Boltzmann-Gesetz in der oben angegebenen Form. Nicht-schwarze KörperDas Stefan-Boltzmann-Gesetz gilt in der obigen Form nur für Schwarze Körper. Ist ein nicht-schwarzer Körper gegeben, der richtungsunabhängig strahlt (so genannter Lambert-Strahler) und dessen Emissionsgrad
Dabei ist der Emissionsgrad Für einen Strahler, bei dem die Richtungsunabhängigkeit oder die Frequenzunabhängigkeit der Emission nicht gegeben ist, muss zur Bestimmung des hemisphärischen Gesamtemissionsgrads ε(T) das Integral individuell unter Zugrundelegung der betreffenden Gesetzmäßigkeiten berechnet werden. Viele Körper weichen nur wenig vom idealen Lambert-Strahler ab; wenn der Emissionsgrad in dem Frequenzbereich, in dem der Körper einen merklichen Anteil seiner Strahlungsleistung abgibt, nur wenig variiert, lässt sich das Stefan-Boltzmann-Gesetz zumindest näherungsweise anwenden. GeschichtlichesDas Stefan-Boltzmann-Gesetz wurde im Jahr 1879 von Josef Stefan experimentell entdeckt und 1884 von Ludwig Boltzmann theoretisch durch thermodynamische Überlegungen aus der klassischen elektromagnetischen Theorie der Strahlung hergeleitet. Im Jahre 1900, also 21 Jahre nach dem Stefan-Boltzmann-Gesetz, entdeckte Max Planck das nach ihm benannte plancksche Strahlungsgesetz, aus dem das Stefan-Boltzmann-Gesetz einfach durch Integration über alle Richtungen und Wellenlängen folgt. Das plancksche Strahlungsgesetz konnte mit der Einführung des Wirkungsquantums h auch erstmals die Stefan-Boltzmann-Konstante auf fundamentale Naturkonstanten zurückführen. BeispielAußerhalb der Erdatmosphäre empfängt eine zur Sonne ausgerichtete Fläche eine Bestrahlungsstärke von S = 1,367 kW/m2 (Solarkonstante). Man bestimme die Temperatur T der Sonnenoberfläche unter der Annahme, dass die Sonne in hinreichender Näherung ein Schwarzer Körper sei. Der Sonnenradius beträgt R = 6,963·108m, der mittlere Abstand zwischen Erde und Sonne ist D = 1,496·1011 m. Die von der Sonnenoberfläche abgegebene Strahlungsleistung P durchdringt eine konzentrisch um die Sonne gelegte Kugelschale des Radius D mit der Bestrahlungsstärke S, beträgt also insgesamt P=4πD2·S = 3,845·1026 W (Leuchtkraft der Sonne). Nach dem Stefan-Boltzmann-Gesetz beträgt die Temperatur der abstrahlenden Oberfläche Die so bestimmte Temperatur der Sonnenoberfläche heißt Effektivtemperatur. Es ist die Temperatur, die ein gleich großer Schwarzer Körper haben müsste, um dieselbe Strahlungsleistung abzugeben wie die Sonne. Siehe auchDas Stefan-Boltzmann-Gesetz macht eine Aussage über die von einem Schwarzen Körper auf allen Frequenzen insgesamt abgegebene Strahlungsleistung. Die Aufteilung auf einzelne Frequenzen bzw. Wellenlängen wird vom planckschen Strahlungsgesetz beschrieben. Das Wiensches Verschiebungsgesetz verbindet die Temperatur eines Schwarzen Körpers mit der am stärksten abgestrahlten Wellenlänge. Literatur
Kategorien: Thermodynamik | Atomphysik |
|||
| Dieser Artikel basiert auf dem Artikel Stefan-Boltzmann-Gesetz aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |




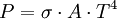
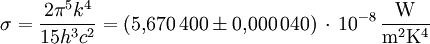 .
.
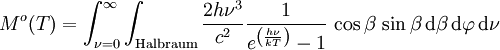 .
.
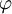 gegebene Richtung nur die auf dieser Richtung senkrecht stehende Projektion
gegebene Richtung nur die auf dieser Richtung senkrecht stehende Projektion 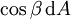 der Fläche
der Fläche 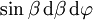 ist ein Raumwinkelelement.
ist ein Raumwinkelelement.
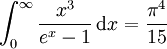 .
.
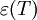 für alle Frequenzen denselben Wert hat (so genannter Grauer Körper), dann ist die von diesem abgegebene Strahlungsleistung
für alle Frequenzen denselben Wert hat (so genannter Grauer Körper), dann ist die von diesem abgegebene Strahlungsleistung
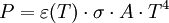
![T = \sqrt[4]{\frac{P}{\sigma A}} = \sqrt[4]{\frac{S \cdot 4 \pi D^2}{\sigma \cdot 4 \pi R^2}} = \sqrt[4]{\frac{S \cdot D^2}{\sigma \cdot R^2}} = \sqrt[4]{\frac{1\,367 \cdot 2{,}238 \cdot 10^{22}}{5{,}670 \cdot 10^{-8} \, \cdot \, 4{,}844 \cdot 10^{17}}} \; \mathrm{K} = 5\,777 \, \mathrm{K}](images/math/b/6/c/b6cb4a7f8b7b0f9591610d0e0bc7d86e.png)


