Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Boltzmann-GleichungDie Boltzmann-Gleichung, auch Boltzmannsche Transportgleichung, ist die grundlegende Integro-Differentialgleichung der kinetischen Gastheorie. Produkt-HighlightSie ist eine Gleichung für die statistische Verteilung von Teilchen in einem Medium. Eine wichtige Anwendung, die durch die Boltzmann-Gleichung beschrieben wird, ist etwa eine Strömung in einem verdünnten Gas. In der Praxis tritt dies zum Beispiel bei der Berechnungen von Phänomenen in der äußeren Atmosphäre auf, wie etwa beim Wiedereintritt des Space Shuttles in die Erdatmosphäre. Die Boltzmann-Gleichung wird dann verwendet, wenn die mittlere freie Weglänge der Teilchen groß ist, d. h. wenn nur wenige Gasteilchen in einem gegebenen Volumen vorhanden sind. In einem Medium, in dem dies nicht der Fall ist, kann man die wesentlich einfacheren Gleichungen der Kontinuumsmechanik verwenden (Navier-Stokes-Gleichung). In diesem Sinne ist die Boltzmann-Gleichung eine mesoskopische Gleichung, die zwischen der mikroskopischen Beschreibung einzelner Teilchen und der makroskopischen Beschreibung steht. GleichungDie Boltzmann-Gleichung ist eine Gleichung für die Verteilungsdichte f(x,v,t). Hier ist x die Ortsvariable, t die Zeitvariable, und v die Geschwindigkeit. Die Verteilungsdichte kann man so interpretieren, dass der Wert f(x,v,t)dxdv, die relative Anzahl der Teilchen angibt, die sich zum Zeitpunkt t im Ortsvolumen [x,x + dx] befinden und dabei die Geschwindigkeiten im Bereich [v,v + dv] haben. Die Gleichung hat die Form (F sei eine gegebene Kraft)
wobei coll(f) das Kollisionsintegral ist. Dieser Term ist ein mehrdimensionales Integral, in dem f nichtlinear verknüpft ist. Er gibt den Beitrag zur Gleichung, der durch Kollision der einzelnen Teilchen entsteht. (Wäre er nicht vorhanden, erlaubte das eine Lösung der Gleichung mit Mitteln der klassischen Mechanik). In engerem Sinn versteht man unter der Boltzmann-Gleichung die obige Gleichung zusammen mit einem speziellen Ansatz für das Kollisionsintegral (Boltzmannscher Stoßzahlansatz):
Dabei ist W(v1,v2;v3,v4) die Übergangswahrscheinlichkeit für Die linke Seite der Boltzmann-Gleichung ist im Grunde nur die ausführliche Schreibweise für die totale Zeitableitung von f. Der zweite Term heißt auch Transportterm und der dritte Feldterm, da er die Wechselwirkung mit äußeren Feldern beschreibt. Sowohl die theoretische als auch die numerische Behandlung der Gleichung ist sehr aufwendig. Es gibt allerdings die bemerkenswerte Grenzwerteigenschaft, dass (unter gewissen Bedingungen) die Boltzmann-Gleichung in die Navier-Stokes-Gleichung übergeht, wenn die mittlere freie Weglänge klein wird. |
| Dieser Artikel basiert auf dem Artikel Boltzmann-Gleichung aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





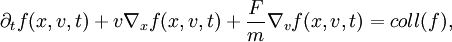
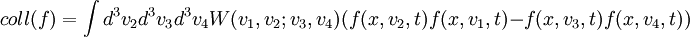
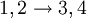 .
.


