Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Bredtsche Formel
Die Bredtschen Formeln sind elementarer Bestandteil der Festigkeitslehre. Sie bilden eine Grundlage zur Berechnung von Schubspannungen und Verformungen bei Bauelementen mit geschlossenen dünnwandigen Hohlquerschnitten unter reiner Torsionsbeanspruchung. In weiterer Folge lassen sich damit auch Torsionswiderstände und Schubmittelpunkte berechnen. Die Formeln stammen ursprünglich von Rudolf Bredt, der sie 1896 im VDI-Journal veröffentlichte[1] . Produkt-Highlight
1. Bredtsche Formel
2. Bredtsche Formel
TorsionswiderstandAus den Bredtschen Formeln lässt sich eine Formel für die Ermittlung des Torsionswiderstandes dünnwandiger geschlossener Profile herleiten. Oft wird auch diese Formel als 2. Bredtsche Formel bezeichnet.
Quellen
|
|||||||||||||
| Dieser Artikel basiert auf dem Artikel Bredtsche_Formel aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





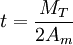
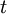
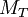
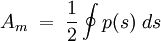
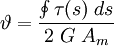
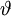
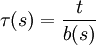
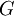
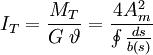
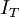 : Torsionswiderstand (Torsionsflächenmoment 2. Grades)
: Torsionswiderstand (Torsionsflächenmoment 2. Grades)


