Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Hilbertraum
Ein Hilbertraum (auch Hilbert-Raum), benannt nach dem Mathematiker David Hilbert, ist ein vollständiger Vektorraum mit Skalarprodukt. Die Dimension eines Hilbertraums ist in den meisten Anwendungen unendlich, jedoch kann sie auch endlich sein (siehe Beispiele). Der Hilbertraum ist ein Spezialfall eines Innenproduktraums (= Prähilbertraums), d. h. ein Vektorraum über den reellen Zahlen oder den komplexen Zahlen mit einem Skalarprodukt (= Innenprodukt). Das Skalarprodukt induziert eine Norm und eine Metrik. Produkt-Highlight
DefinitionEin Prähilbertraum, der vollständig bezüglich der durch das Skalarprodukt induzierten Metrik ist, in dem also jede Cauchy-Folge konvergiert, heißt Hilbertraum. Insbesondere können Hilberträume auch unendlichdimensional sein, wenn nur die Länge, also NotationIn diesem Artikel werden Variablen für Vektoren nicht gesondert gekennzeichnet, es werden also gewöhnliche kursive Kleinbuchstaben verwendet: u,v,w,x,y. Das Skalarprodukt von u und v wird mit BedeutungDer hohe Grad an mathematischer Struktur in Hilberträumen vereinfacht die Analysis ungemein, und so spielen sie in der Funktionalanalysis, speziell in der Lösungstheorie partieller Differentialgleichungen und damit auch der Physik eine große Rolle. Als Beispiel sei hier die Quantenmechanik genannt, wo die Zustände eines quantentheoretischen Systems einen Hilbertraum bilden. DualraumJeder Hilbertraum ist zugleich ein Banach-Raum und hat so alle dessen Eigenschaften. Insbesondere hat jeder Hilbertraum einen Dualraum. Hier gilt allerdings der Rieszsche Darstellungssatz: Jeder reelle Hilbertraum ist mittels der Abbildung Die Eigenschaft, dass die kanonische Inklusion eines Raumes in seinen Bidualraum ein isometrischer Isomorphismus ist, nennt man Reflexivität. Nach dem oben genannten Satz sind also alle Hilberträume reflexiv. Beispiele für Hilberträume
OrthogonalitätZwei Elemente des Hilbertraumes heißen orthogonal zueinander, wenn ihr Skalarprodukt 0 ergibt. Eine Familie von paarweise orthogonalen Vektoren heißt Orthogonalsystem. Unter den Orthogonalsystemen spielen die Orthogonalbasen eine besondere Rolle: das sind Orthogonalsysteme, die nicht mehr durch Hinzufügen eines weiteren Vektors vergrößert werden können, also bezüglich Inklusion maximal sind. Äquivalent dazu ist, dass die lineare Hülle im Hilbertraum dicht ist. Außer im Falle von endlichdimensionalen Räumen bilden Orthogonalbasen keine Basis im üblichen Sinn der linearen Algebra (Hamelbasis). Sind diese Basisvektoren darüber hinaus so normiert, dass das Skalarprodukt eines Vektors mit sich selbst 1 ergibt, so spricht man von einem Orthonormalsystem bzw. einer Orthonormalbasis.
Die Vektoren
vi bilden also genau dann ein Orthonormalsystem, wenn Jeder Hilbertraum besitzt eine Orthonormalbasis. Es kann sogar jedes Orthonormalsystem zu einer Orthonormalbasis ergänzt werden. FourierkoeffizientEine Orthonormalbasis ist ein mächtiges Hilfsmittel bei der Untersuchung von Hilberträumen und ihren Elementen. Insbesondere bietet eine Orthonormalbasis eine einfache Möglichkeit, die Darstellung eines Vektors durch die Elemente der Orthonormalbasis zu bestimmen. Sei Da B eine Basis des Raumes bildet, gibt es Koeffizienten ak mit Der n-te Basiskoeffizient der Darstellung eines Vektors in einer Orthonormalbasis kann also durch Skalarproduktbildung ermittelt werden. Diese Koeffizienten werden auch Fourierkoeffizienten genannt, da sie eine Verallgemeinerung des Konzeptes der Fourieranalyse darstellen. Akademischer HumorAn mehreren deutschsprachigen Universitäten gibt es als „Hilbertraum“ bezeichnete Räumlichkeiten; an der Georg-August-Universität in Göttingen etwa, an der David Hilbert lange Jahre lehrte und forschte, trägt das Foyer des mathematischen Institutes, in dem eine Büste des Mathematikers aufgestellt ist, diesen Namen. An der Universität Karlsruhe (TH) ist es unter den (selbst studentischen) Organisatoren der Einführungsveranstaltungen für die neuen Erstsemesterstudierenden der Fakultät für Physik üblich, den neuen Studenten im Rahmen einer Campus-Rally die Aufgabe zu stellen, den "Hilbert"-Raum zu finden. Gemeint ist das Büro eines Physik-Professors, der mit Vornamen Hilbert heißt. Siehe auchTabelle mathematischer Symbole
|
||||||||||||||
| Dieser Artikel basiert auf dem Artikel Hilbertraum aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





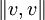 (|| || ist die Metrik), jedes Vektors aus diesem Raum endlich ist.
(|| || ist die Metrik), jedes Vektors aus diesem Raum endlich ist.
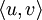 bezeichnet. Im komplexen Fall folgt der Artikel der in der Physik fast ausschließlich verbreiteten Konvention, dass das Skalarprodukt im ersten Argument semilinear ist, im zweiten linear:
bezeichnet. Im komplexen Fall folgt der Artikel der in der Physik fast ausschließlich verbreiteten Konvention, dass das Skalarprodukt im ersten Argument semilinear ist, im zweiten linear:
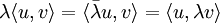
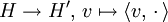 isometrisch isomorph zu seinem (topologischen) Dualraum. Im Falle eines komplexen Hilbertraums ist diese Abbildung aber nur semilinear. In beiden Fällen ist der Hilbertraum isometrisch isomorph zu seinem Bidualraum. Dieser Satz hat weitreichende Konsequenzen.
isometrisch isomorph zu seinem (topologischen) Dualraum. Im Falle eines komplexen Hilbertraums ist diese Abbildung aber nur semilinear. In beiden Fällen ist der Hilbertraum isometrisch isomorph zu seinem Bidualraum. Dieser Satz hat weitreichende Konsequenzen.
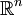 mit dem Standardskalarprodukt
mit dem Standardskalarprodukt 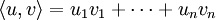 .
.
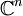 mit
mit 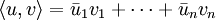 .
.
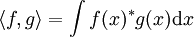 . Eine exaktere Definition, die insbesondere die Vollständigkeit näher beleuchtet, findet sich im Artikel über Lp-Räume. Ein Beispiel eines solchen Raumes ist der oben genannte Raum der
. Eine exaktere Definition, die insbesondere die Vollständigkeit näher beleuchtet, findet sich im Artikel über Lp-Räume. Ein Beispiel eines solchen Raumes ist der oben genannte Raum der 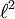 aller Folgen mit der Eigenschaft, dass die Summe der Quadrate aller Folgenglieder endlich ist. Dieser ist der ursprüngliche Hilbertraum, anhand dessen David Hilbert die Eigenschaften solcher Räume untersuchte. Weiter ist dieses Beispiel wichtig, weil alle separablen unendlich-dimensionalen Hilberträume isometrisch isomorph zu
aller Folgen mit der Eigenschaft, dass die Summe der Quadrate aller Folgenglieder endlich ist. Dieser ist der ursprüngliche Hilbertraum, anhand dessen David Hilbert die Eigenschaften solcher Räume untersuchte. Weiter ist dieses Beispiel wichtig, weil alle separablen unendlich-dimensionalen Hilberträume isometrisch isomorph zu 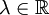 betrachte man die Funktionen
betrachte man die Funktionen 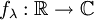 mit
mit 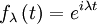 . Durch das Skalarprodukt
. Durch das Skalarprodukt 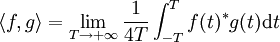 wird der Raum
wird der Raum 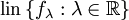 (der von den Funktionen
(der von den Funktionen 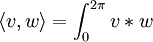 . Dann bilden die Vektoren
. Dann bilden die Vektoren 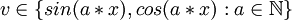 für beliebige a,b eine unendlichdimensionale Orthonormalbasis des Hilbertraumes, da
für beliebige a,b eine unendlichdimensionale Orthonormalbasis des Hilbertraumes, da 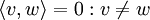 und
und 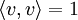 .
.
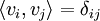 für alle
für alle 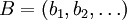 eine Orthonormalbasis und
eine Orthonormalbasis und 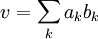 .
Diese Koeffizienten bestimmt man unter Ausnutzung der speziellen Eigenschaften der Orthonormalbasis:
.
Diese Koeffizienten bestimmt man unter Ausnutzung der speziellen Eigenschaften der Orthonormalbasis:
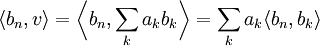 . Da das Skalarprodukt von unterschiedlichen Basisvektoren 0 und von gleichen Basisvektoren 1 ist, erhält man so
. Da das Skalarprodukt von unterschiedlichen Basisvektoren 0 und von gleichen Basisvektoren 1 ist, erhält man so
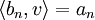 .
.


