Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Parität (Physik)Die Parität bezeichnet in der Physik eine Symmetrieeigenschaft. Produkt-HighlightZur Parität gehört die Symmetrieoperation der Inversion P. Die Inversion (auch Raumspiegelung oder Punktspiegelung) stellt die Spiegelung an einem Punkt dar, dem Inversionszentrum. Befindet sich das Inversionszentrum im Ursprung eines kartesischen Koordinatensystems, so kehrt die Inversion das Vorzeichen aller Koordinaten um (nicht nur einer, wie bei der Spiegelung an der Ebene):
Besitzt ein System eine solche Symmetrie, ist also der Eigenwert des Paritätsoperators +1,
so spricht man von positiver Parität, Inversionsinvarianz, oder kurz P-Invarianz. Da ein solches System bei der Inversion P in sich selbst überführt wird nennt man es inversionssymmetrisch oder gerade. Ändert das System jedoch unter der Inversion P das Vorzeichen, ist also der Eigenwert des Paritätsoperators -1,
so spricht man von negativer Parität und das System ist dann ungerade. In der Quantenmechanik wirkt der Paritätsoperator auf eine Wellenfunktion ψ. Jede gesuchte Wellenfunktion besitzt dabei eine wohldefinierte Parität (in gebundenden Zuständen). Charakteristisch für die Quantenmechanik ist der Paritätsoperator des Dirac-Formalismus, der die Ortskoordinate q durch -q ersetzt. Jede beliebige Wellenfunktion kann in einen Anteil mit gerader und einen mit ungerader Parität zerlegt werden. Das entspricht im übrigen dem Entwicklungssatz, nach dem jeder beliebige Zustand nach den Eigenzuständen eines hermiteschen Operators entwickelt werden kann. Die Inversion überführt rechtshändige Systeme in linkshändige, und umgekehrt (genaugenommen ist dies nur in Räumen mit ungeradzahliger Dimensionalität der Fall). Beim Verhalten unter Inversion unterscheiden sich axiale Vektoren von polaren Vektoren. Die schwache Wechselwirkung ist nicht invariant unter Inversion. Dies wurde zuerst 1956 im Wu-Experiment (nach Chien-Shiung Wu) gezeigt und erschütterte die bis dahin vorherrschende Überzeugung, dass alle Naturgesetze inversionsinvariant sind. Siehe auch
|
| Dieser Artikel basiert auf dem Artikel Parität_(Physik) aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





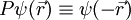 .
.
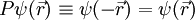 ,
,
 ,
,


