Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Ritzsches VariationsverfahrenDas Ritzsche Variationsverfahren ist eine einfache Methode, um den quantenmechanischen Grundzustand eines Systems abzuschätzen. Dabei wird benutzt, dass der Erwartungswert des Hamiltonoperators bezüglich einer (parametrisierten) Testfunktion immer größer ist als die Grundzustandsenergie. Dies zeigt man leicht, indem man den Hamiltonoperator in einer Eigenbasis darstellt und dann den Erwartungswert bezüglich der Testfunktion abschätzt: Weiteres empfehlenswertes FachwissenIn der Praxis wählt man Testfunktionen mit einem(oder mehreren) Parametern, und variiert dann den Rayleigh-Koeffizienten
|
| Dieser Artikel basiert auf dem Artikel Ritzsches_Variationsverfahren aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


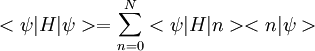
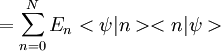
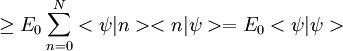



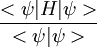 nach diesen. Das Minimum dieser Variation ist dann die beste Abschätzung für unsere Grundzustandsenergie
nach diesen. Das Minimum dieser Variation ist dann die beste Abschätzung für unsere Grundzustandsenergie 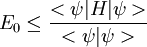 .
.


