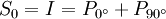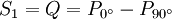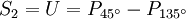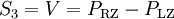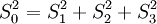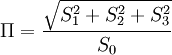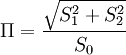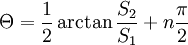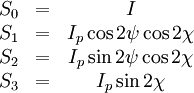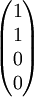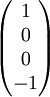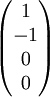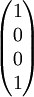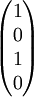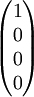Meine Merkliste

Home
Lexikon
Stokes-Parameter

Stokes-Parameter

Die Stokes-Parameter sind ein Satz von vier Werten, meist als S₀…S₃ oder I, Q, U und V bezeichnet, die 1852 von George Gabriel Stokes zur Beschreibung des Polarisationszustandes elektromagnetischer Wellen (meist Licht) eingeführt wurden. Das Besondere an diesen Werten ist, dass sie durch einfache Messungen der Lichtleistung nach Durchgang durch verschiedene Polarisatoren berechnet werden können und so der Polarisationszustand recht einfach bestimmt werden kann.

Weiteres empfehlenswertes Fachwissen

Wie kann man Pipetten schnell überprüfen?

Sicherer Wägebereich zur Sicherstellung genauer Resultate

Was ist die Empfindlichkeit meiner Waage?

Die vier Stokes-Parameter S₀…S₃ können zum sog. Stokes-Vektor zusammengefasst werden.

Definition

$S_0 = I = P_{0^\circ}+P_{90^\circ}$

$S_1 = Q = P_{0^\circ}-P_{90^\circ}$

$S_2 = U = P_{45^\circ}-P_{135^\circ}$

$S_3 = V =P_{\rm RZ} - P_{\rm LZ}\,$

Die Leistungen sind dabei die gemessene Leistung nach Durchgang durch einen horizontal (0°), vertikal (90°), 45° und 135° orientierten Polarisator sowie der rechts- und links-zirkular polarisierte Anteil des Lichts.

Üblicherweise werden die Stokes-Parameter auf die einfallende Leistung normiert, indem alle vier Werte durch S₀ dividiert werden.

Für vollständig polarisiertes Licht gilt:

$S_0^2=S_1^2+S_2^2+S_3^2$

Für unpolarisiertes Licht hingegen gilt $S 1 = S 2 = S 3 = 0$ . Es lässt sich ein Polarisationsgrad Π definieren durch:

$\Pi=\frac{\sqrt{S_1^2+S_2^2+S_3^2}}{S_0}$

Beziehungsweise für nur linear polarisiertes Licht:

$\Pi=\frac{\sqrt{S_1^2+S_2^2}}{S_0}$

Der Winkel der maximalen Polarisation ist definiert durch:

$\Theta=\frac{1}{2} \arctan{\frac{S_2}{S_1}}+n \frac{\pi}{2}$

wobei $n = 1$ für $S 1 < 0$ , ansonsten ist $n = 0$ . Anders ausgedrückt bedeutet das, dass man 90° zum Winkel $Θ$ hinzu zählen muss, wenn $S 1$ kleiner als $0$ ist.

Eine andere Formulierung findet sich in Kugelkoordinaten:

$\begin{matrix} S_0 &=& I \\ S_1 &=& I_p \cos 2\psi \cos 2\chi\\ S_2 &=& I_p \sin 2\psi \cos 2\chi\\ S_3 &=& I_p \sin 2\chi \end{matrix}$

Wobei $I$ die Gesamtintensität, $I p$ der polarisierte Anteil der Intensität, $ψ$ die Verkippung der Polarisationsellipse und $tanχ$ das Verhältnis der beiden Hauptachsen der Polarisationsellipse ist.

Beispiele

Polarisation	Stokes-Vektor	Polarisation	Stokes-Vektor
linear, horizontal	$\begin{pmatrix} 1\\ 1\\ 0\\ 0 \end{pmatrix}$	links-zirkular	$\begin{pmatrix} 1\\ 0\\ 0\\ -1 \end{pmatrix}$
linear, vertikal	$\begin{pmatrix} 1\\ -1\\ 0\\ 0 \end{pmatrix}$	rechts-zirkular	$\begin{pmatrix} 1\\ 0\\ 0\\ 1 \end{pmatrix}$
linear, +45°	$\begin{pmatrix} 1\\ 0\\ 1\\ 0 \end{pmatrix}$	unpolarisiert	$\begin{pmatrix} 1\\ 0\\ 0\\ 0 \end{pmatrix}$

Literatur

Craig F. Bohren, Donald R. Huffman: Absorption and scattering of light by small particles. Wiley, New York 1998, ISBN 0-471-29340-7.

Kategorie: Elektrodynamik

Dieser Artikel basiert auf dem Artikel Stokes-Parameter aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar.