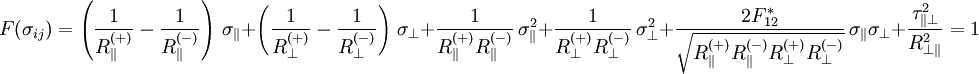Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Tsai-Wu KriteriumDas Tsai-Wu Kriterium gehört zu den nicht-differenzierenden Versagenskriterien bzw. Pauschalkriterien für Faser-Kunststoff-Verbund. Es geht zurück auf Stephen W. Tsai und Edward M. Wu, die es 1971 für ebene Spannungszustande veröffentlichten. Kennzeichnend für diese Werkstoffe ist ihre strukturelle Anisotropie im Vergleich zu homogenen Werkstoffen, die weitgehend isotropes Werkstoffverhalten aufweisen. Vollständig lässt sich daher ein Faserverbundwerkstoff nur beschreiben, wenn neben den Elastizitäten auch die Materialfestigkeiten, also das Werkstoffversagen richtungsabhängig beschreibbar sind. Produkt-Highlight
Mathematische HerleitungDas Tsai-Wu Kriterium beschreibt einen Bruchkörper im 6 dimensionalen Spannungsraum σij (σx, σy, σz, τxz, τyz, τxy). Versagen wird dann vorhergesagt, wenn der Spannungszustand außerhalb der Bruchfläche des Bruchkörpers liegt. Alle Spannungszustände innerhalb des Bruchkörpers sind versagensfrei. Mathematisch kann ein beliebiger Bruchkörper im Spannungsraum durch eine Funktion
beschrieben werden. Das mitunter bekannteste Kriterium im Faserverbundleichtbau dieser Art ist das
Tsai-Wu Kriterium, das auf eine Reihenentwicklung von allen Spannungskoeffizienten (σij) und anisotropen Festigkeitskoeffizienten (aij, bijkl, cijklmn,
dargestellt werden. Das Tasi-Wu Kriterium ist nun letztlich ein Spezialfall bei dem nur die ersten zwei Glieder der Reihenentwicklung berücksichtigt werden. Wird weiterhin für die Exponenten α = β = 1 angenommen, ergibt sich das Tsai-Wu Kriterium in der Form
Bestimmung der FestigkeitenDie Festigkeitstensoren aij und bijkl müssen den anisotropen Festigkeitseigenschaften von Faserverbundwerkstoffen angepasst werden. Werden lediglich die zweidimensionalen, ebenen Werkstoffeigenschaften, also nur die Indizes 1 und 2 sowie für die Festigkeitskoeffizienten aij und bijkl eine transversal isotrope Materialsymmetrie berücksichtigt, vereinfacht sich die Gleichung zu
Die Festigkeitskoeffizienten sollen nun aus Standardversuchen (Zug, Druck, Schub) bestimmt werden, dazu werden die Festigkeiten aus uniaxiale Belastungen längs (
Der Koeffizient Tsai-Wu KriteriumAusgeschrieben ergibt sich das Festigkeitskriterium nach Tsai-Wu zu:
mit
Fazit, DiskussionDas Tsai-Wu Kriterium ist ein überschaubarer Ansatz, um richtungsabhängige Materialfestigkeiten zu berücksichtigen. Attraktivität gewinnt dieses Kriterium durch die einfache Umsetzbarkeit und Übersichtlichkeit. Im Gegensatz zu anderen Kriterien verfügt das Tsai-Wu Kriterium über keine Auskunft für verschiedene Bruchmoden. So wird Zwischenfaserbruch (Zfb), Faserbruch(Fb) sowie Versagen unter Druck- und Zugbeanspruchungen in einem Kriterium bestimmt. Diese Eigenschaft des Kriteriums wird als Nachteil angesehen, da der Konstrukteur keine Auskunft über den Bruchmode erhält. Dementsprechend erhält man keine Information, wie die Auslegung eines Bauteils zu verändern ist, um Versagen zu vermeiden. Siehe auch
Veröffentlichungen und Beiträge
|
|
| Dieser Artikel basiert auf dem Artikel Tsai-Wu_Kriterium aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |




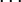 ) zurückgeht. Beschränkt man sich bei der mathematischen Darstellung auf die Einsteinsche Summenkonvention, dann kann eine Reihenentwicklung in der Form
) zurückgeht. Beschränkt man sich bei der mathematischen Darstellung auf die Einsteinsche Summenkonvention, dann kann eine Reihenentwicklung in der Form
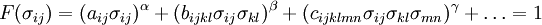
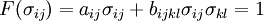
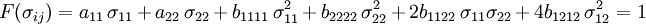
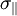 ) und quer (
) und quer (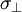 )
zur Faserrichtung bestimmt. Mit den Druck-
)
zur Faserrichtung bestimmt. Mit den Druck- 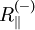 und Zugfestigkeiten
und Zugfestigkeiten 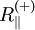 in Faserrichtung sowie den Druck-
in Faserrichtung sowie den Druck- 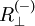 und Zugfestigkeiten
und Zugfestigkeiten 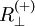 quer zur Faserrichtung und den Schubfestigkeiten
quer zur Faserrichtung und den Schubfestigkeiten 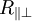 berechnen sich die Koeffizienten der tensoriellen
Festigkeitskennwerte folgender maßen:
berechnen sich die Koeffizienten der tensoriellen
Festigkeitskennwerte folgender maßen:
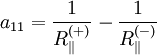
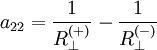
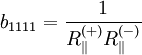
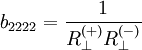
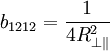
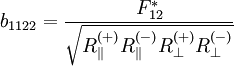
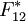 von Tsai als Interaktionskoeffizient bezeichnet, kann aus einer
kombinierten biaxialen normal Belastung
von Tsai als Interaktionskoeffizient bezeichnet, kann aus einer
kombinierten biaxialen normal Belastung 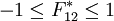 vor.
vor.