Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Unidirektionale SchichtUnidirektionale Schicht (kurz: UD-Schicht) ist die Bezeichnung für eine Schicht eines Faser-Kunststoff-Verbunds, in welcher alle Fasern in eine einzige Richtung orientiert sind. Die Fasern werden dabei als ideal parallel und homogen verteilt angenommen. Die unidirektionale Schicht ist transversal isotrop. Die UD-Schicht ist das Grundelement geschichteter Faser-Kunststoff-Verbunde. Produkt-Highlight
AnwendungDie UD-Schicht ist das Grundelement von geschichteten Faser-Kunststoff-Verbunden. Dies betrifft sowohl die Berechnung der elastischen Eigenschaften mit Hilfe der klassischen Laminattheorie, der Netztheorie als auch die Festigkeitsberechnung (Bruchkriterien für Faserkunststoffverbunde).
Die UD-Schicht stellt hinsichtlich ihrer Steifigkeit und Festigkeit das Ideal einer faserverstärkten Schicht dar. Daher werden die Steifigkeits- und Festigkeitseigenschaften von UD-Schichten oft abgemindert. Insbesondere die Annahme der ideal gestreckten Faser trifft in der Realität oft nicht zu. Wellige Schichten haben aber insbesondere eine niedrige Paralleldruckfestigkeit Mechanische Eigenschaften der UD-SchichtDie UD-Schicht ist, unabhängig vom verwendeten Faser- oder Matrixtyp, transversal isotrop. Auch UD-Schichten, die aus einer isotropen Faser (z. B. Glasfaser) bestehen, ergeben eine orthotrope Elastizität. Die transversale Isotropie ist eine Sonderform der rhombischen Anisotropie oder Orthotropie. Bei der transversalen Isotropie ist eine Symmetrieebene des Werkstoffs gegenüber der Drehung invariant. Wird die UD-Schicht außerhalb ihrer Orthotropieachsen belastet, zeigt sie anisotropes Verhalten. Die transversale Isotropie der UD-Schicht ist durch das Fehlen der Schiebungs-Dehnungs-Kopplung, eines richtungsabhängigen Elastizitätsmoduls sowie der Invarianz gegenüber der Drehung um die Faserachse gekennzeichnet. IndizierungDie Beschreibung der UD-Schicht erfolgt in einem physikalischen International ist die 1,2,3-Indizierung üblich. Im englischsprachigen Raum wird jedoch oft eine andere Indizierung der Querkontraktionszahlen benutzt. Da die Querkontraktionszahlen Berechnung der GrundelastizitätsgrößenDie Grundelastizitätsgrößen einer UD-Schicht berechnen sich aus den Elastizitätsgrößen von Faser und Matrix auf mikromechanischer Basis. Entsprechend ihrem Faservolumenanteil gehen die Elastizitätsgrößen in die Gesamtsteifigkeit ein. Dabei wird in eine Reihenschaltung oder Parallelschaltung der Steifigkeiten unterschieden. Die elastischen Kennwerte des orthotropen Materials lassen sich aufgrund der Symmetrie in der 2-3-Ebene reduzieren auf die E-Moduln Die unabhängigen Elastizitätsgrößen sind der UD-Schicht eigen und können auf keinem anderen Weg berechnet werden. Alternativ können sie in Versuchen gemessen werden. Dies erweist sich jedoch, besonders im Fall der Querkontraktionszahlen, als schwierig. Daher wird überwiegend der Berechnungsweg über die Mikromechanik gewählt. Um Effekte wie die Dehnungsvergrößerung zu berücksichtigen, sind eine Reihe von Korrekturen notwendig, die jedoch in der Mikromechanik berücksichtigt werden. Berechnungverfahren können der Literatur entnommen werden. Die abhängigen Elastizitätsgrößen werden aus den unabhängigen Elastizitätsgrößen berechnet. Unabhängige GrundelastizitätsgrößenDie folgenden Grundelastizitätsgrößen sind notwendig, um eine UD-Schicht vollständig zu beschreiben.
Anders als bei isotropen Werkstoffen lässt sich der Schubmodul Der Elastizitätsmodul in faserparalleler Richtung Abhängige GrundelastizitätsgrößenAus den unabhängigen Elastizitätsgrößen können die fehlenden abhängigen Elastizitätsgrößen berechnet werden. Der Schubmodul in der transversal isotropen Ebene berechnet sich wie im Isotropen aus: SteifigkeitsmatrixMit Hilfe der abhängigen und unabhängigen Elastizitätsgrößen lässt sich die Steifigkeitsmatrix für den ebenen Spannungsfall aufstellen.
Die Matrix für den räumlichen Spannungsfall ergibt sich analog. Transformation
Mit Hilfe der Polartransformation kann die Steifigkeitsmatrix der UD-Schicht um die 3-Achse (Achse normal zur Schichtebene) gedreht werden. Damit ist z. B. der Aufbau eines ausgeglichenen Winkelverbunds möglich. Die Polartransformation um einen Winkel Anwendung in der Finite-Elemente-MethodeDie Grundelastizitätsgrößen können in allen gängigen FEM-Programmen genutzt werden, um das orthotrope bzw. anisotrope Verhalten einer UD-Schicht zu beschreiben. Es muss jedoch auf eine ausreichend feine Diskretisierung in Schichtdickenrichtung geachtet werden. |
|
| Dieser Artikel basiert auf dem Artikel Unidirektionale_Schicht aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





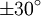 .
.
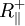 .
.
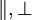 -Koordinatensystem, bzw. im 1,2,3-System. Dabei entspricht 1 und
-Koordinatensystem, bzw. im 1,2,3-System. Dabei entspricht 1 und 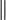 der faserparallelen Richtung und 2, 3 bzw.
der faserparallelen Richtung und 2, 3 bzw. 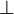 der fasersenkrechten Richtung. Die Orthotropieachsen fallen mit den Koordinatenachsen zusammen.
der fasersenkrechten Richtung. Die Orthotropieachsen fallen mit den Koordinatenachsen zusammen.
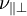 und
und 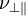 nicht identisch sind, kann es hier schnell zu Irrtümern kommen. Die Querkontraktionszahl
nicht identisch sind, kann es hier schnell zu Irrtümern kommen. Die Querkontraktionszahl 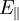 und
und 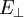 ,
, 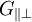 und
und 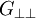 und
und 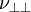 . Diese lassen sich unterteilen in unabhängige und abhängige Elastizitätsgrößen.
. Diese lassen sich unterteilen in unabhängige und abhängige Elastizitätsgrößen.
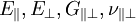
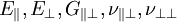
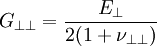 . Die zweite Querkontraktionszahl
. Die zweite Querkontraktionszahl 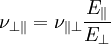 berechnet.
berechnet.
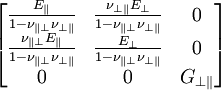
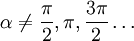 führt zur Anisotropie in der UD-Schicht und damit zur Dehnungs-Schiebungs-Kopplung.
führt zur Anisotropie in der UD-Schicht und damit zur Dehnungs-Schiebungs-Kopplung.


