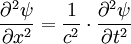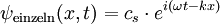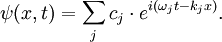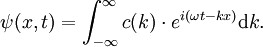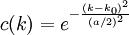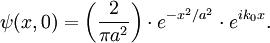Meine Merkliste

Wellenpaket

Ein Wellenpaket oder Wellengruppe ist ein räumlich und zeitlich begrenztes System von Wellen, das ein breites Frequenzband umfasst. Die Frequenzverteilung lässt sich rechnerisch mit Hilfe einer sogenannten Fouriertransformation und experimentell mit einem Spektrometer bestimmen. Dies bedeutet, dass man durch Superposition (Aufaddieren) mehrerer einfacher Wellen erreicht, dass sich die Amplitude nur in einem räumlich eng begrenzten Bereich merklich von 0 unterscheidet.

Die Kombination von Ort und Zeitpunkt, wo die Ausdehnung am kürzesten ist, nennt man Konzentrationspunkt. Je breitbandiger das Wellenpaket im Frequenzbereich ist, desto kürzer ist es im Zeitbereich im Konzentrationspunkt.

Weiteres empfehlenswertes Fachwissen

Empfindlichkeitsprüfung von Laborwaagen

Leitfaden für die Waagenreinigung: 8 einfache Schritte

Leitfaden zu den grundlegenden Laborkenntnissen

Inhaltsverzeichnis

1 Mathematische Formulierung
2 Beispiel: Gauß'sches Wellenpaket
- 2.1 mathematisch
3 Dispersion
4 Anwendung in verschiedenen Gebieten
- 4.1 Wasserwellen
- 4.2 Materiewellen
5 Literatur

Mathematische Formulierung

Ein Wellenpaket soll, genau wie eine einzelne Welle, eine Lösung der allgemeinen Wellengleichung

$\frac{\partial^2\psi}{\partial x^2}=\frac{1}{c^2}\cdot\frac{\partial^2\psi}{\partial t^2}$

sein. Darum geht man von monochromatischen Wellen aus, welche die einfachsten Lösungen dieser Gleichung darstellen.

Eine monochromatische Welle mit Ausbreitung in x-Richtung wird dargestellt durch:

$\psi_{\rm einzeln}(x, t)=c_s\cdot e^{i(\omega t-kx)}$

Physikalisch sinnvoll ist der Realteil oder Imaginärteil (auch $ψ + ψ *$ ):

$Re \psi_{\rm einzeln}(x, t)=c_s\cdot \cos(\omega t-kx)$

Überlagert man nun mehrere solcher monochromatischer Wellen, so ergibt sich eine Struktur im Ortsraum (siehe Abbildung), die Summe ist aber immer noch Lösung der Wellengleichung:

$\psi(x, t)=\sum\limits_j c_j\cdot e^{i(\omega_j t-k_jx)}.$

Man hat weiterhin eine Lösung der Wellengleichung, wenn man von der Summe zum Integral übergeht. Dabei legt c(k) die Amplitude fest, die jetzt von k abhängt:

(1) $\psi(x, t)=\int_{-\infty}^{\infty} c(k)\cdot e^{i(\omega t-kx)} \mathrm dk.$

Beispiel: Gauß'sches Wellenpaket

Ein häufig verwendetes Beispiel für ein Wellenpaket ist das sogenannte Gaußsche Wellenpaket. Hierbei handelt es sich um eine Welle, die mit einer Gaußfunktion moduliert ist. Mathematisch bedeutet dies eine Multiplikation der Wellenfunktion mit einer Gaußfunktion. Eine Besonderheit des Gaußschen Wellenpakets liegt darin, dass die Fouriertransformation einer Gaußfunktion (und damit die Frequenzverteilung) wieder eine Gaußfunktion ergibt.

mathematisch

Setzt man in obiger Gleichung (1) für die Amplitudenverteilung eine Gaußfunktion

$c(k)=e^{-\frac{(k-k_0)^2}{(a/2)^2}}$

ein, so erhält man nach der elementar durchführbaren Integration zum Zeitpunkt $t = 0$ :

$\psi(x, 0)=\left(\frac{2}{\pi a^2}\right)\cdot e^{-x^2/a^2}\cdot e^{ik_0x}.$

Nebenstehende Abbildung zeigt das Ergebnis. Man hat jetzt nur noch einen Bereich, in dem die Amplitude merklich von 0 verschieden ist.

Dispersion

Ist die Ausbreitungsgeschwindigkeit der Welle frequenzabhängig (z.B. Licht in Materie) "zerläuft" das Wellenpaket, d.h. seine Breite wird mit der Zeit immer größer und die räumliche Bestimmtheit immer ungenauer. Siehe auch Dispersion.

Anwendung in verschiedenen Gebieten

Wasserwellen

Wellenpakete kommen als Oberflächenwellen in Wasser zur Anwendung, beispielsweise um die Übertragungsfunktionen (engl.: RAO = Response Amplification Operator) von Schiffen und Offshore-Konstruktionen im Modellversuch zu messen. Dass sich alle Wellen, die von der Wellenmaschine ausgehen, zur gleichen Zeit am gleichen Ort treffen gelingt nur, weil nach der Dispersionsrelation sich kurze (hochfrequente) Wellen auf der Wasseroberfläche langsamer ausbreiten als lange (niederfrequente) Wellen. Als Dienstleister für solche Modellversuche treten (wenige) Schiffbau-Versuchsanstalten auf.

Materiewellen

In der Quantenmechanik verwendet man Wellenpakete, um Teilchen im Wellenbild darzustellen. Die Breite eines Wellenpaketes im Orts- und Impulsraum ist dabei über die heisenbergsche Unschärferelation verknüpft. Ein örtlich gut bestimmtes Teilchen hat demnach eine sehr breite Impulsverteilung und umgekehrt. Das gleiche gilt für Energie (Frequenz) und Zeit.

Literatur

Wolfgang Demtröder: Experimentalphysik 3. Atome, Moleküle und Festkörper. 2. Auflage, Springer Verlag. New York - Berlin - Heidelberg 2002.

Kategorie: Quantenphysik

Dieser Artikel basiert auf dem Artikel Wellenpaket aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar.