Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Zustandsgleichung von Birch-MurnaghanDie Zustandsgleichung nach Birch-Murnaghan beschreibt die Beziehung zwischen dem Volumen V eines Festkörpers und des auf ihn wirkenden äußeren hydrostatischen Drucks p. Diese Zustandsgleichung ist von zwei Parametern abhängig, dem Kompressionsmodul bei einem Druck von 0 GPa K0, und der ersten Ableitung des Kompressionsmoduls nach dem Druck bei einem Druck von 0 GPa, K0'. Diese sind wie folgt definiert: Produkt-HighlightMurnaghan ging davon aus, dass der Kompressionsmodul eines Festkörpers K0 linear mit dem auf ihn wirkenden Druck zunimmt. Eine weitere wichtige Annahme ist, dass die Grösse K0' druckunabhängig ist.
Nach Integration erhält man die Zustandsgleichung nach Murnaghan bzw. wobei V0 das Volumen des Festkörpers bei einem Druck von 0 GPa ist. Einen anderen Weg, das Verhalten von kondensierter Materie unter Druck zu beschreiben, wurde von Birch eingeschlagen. Er ging davon aus, dass nach den Maxwell-Relationen ein Zusammenhang zwischen dem Druck p und der freien Energie F besteht: Birch stellte die freie Energie eines Festkörpers als Reihenentwicklung dar: Hier sind an druckabhängige Koeffizienten, εn ist die sog. Eulersche Dehnung. Nach einer Reihenentwicklung, deren Darstellung in diesem Rahmen zu weit führen würde, erhält man dann die Zustandsgleichung nach Birch: Es hat sich mittlerweile eingebürgert, diese Gleichung als Zustandsgleichung nach Birch-Murnaghan zu bezeichnen, auch wenn der Ansatz von Birch mit dem Ansatz von Murnaghan nichts gemein hat. Literatur
Kategorien: Festkörperphysik | Zustandsgleichung |
| Dieser Artikel basiert auf dem Artikel Zustandsgleichung_von_Birch-Murnaghan aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


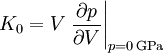
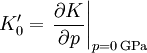



![p = \frac{K_0}{K_0'}\left[\left(\frac{V}{V_0}\right)^{K_0'} - 1\right]](images/math/c/c/9/cc976d2b244d1f1111ad4c5891be3fa9.png)
![\frac{V}{V_0} = \left[\frac{K_0'}{K_0}p+1\right]^{-\frac{1}{K_0'}}](images/math/a/0/4/a041cecab466fbaf9aa753a309158a0d.png)
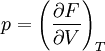
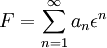
![\epsilon = \frac{1}{2}\left[1 - \left(\frac{V}{V_0}\right)^{-\frac{2}{3}}\right]](images/math/5/5/9/559df4caf94b312cc4efbf2440aba070.png)
![p = \frac{3}{2} K_0 \left[\left(\frac{V}{V_0}\right)^{-\frac{7}{3}} + \left(\frac{V}{V_0}\right)^{-\frac{5}{3}}\right]\left[1 + \frac{3}{4}\left(K_0' - 4\right)\left[\left(\frac{V}{V_0}\right)^{-\frac{2}{3}}-1\right]\right]](images/math/f/d/f/fdf3f51df89249e8997b488d717b2703.png)


