Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
BinärpräfixBinärpräfixe sind Vorsätze für Maßeinheiten (Einheitenvorsätze), die zur Bezeichnung von auf Zweierpotenzen basierenden Vielfachen einer Maßeinheit dienen. Sie werden vorwiegend mit den Einheiten Bit (Symbol „bit“, auch „b“) oder Byte (Symbol „B“) verwendet, um Datenmengen zu quantifizieren, da Datenspeicher aus technischen Gründen oft eine als Zweierpotenz darstellbare Speicherkapazität besitzen. Die Binärpräfixe ergänzen die etablierten, auf Zehnerpotenzen basierenden SI-Präfixe. Produkt-Highlight
Standardisierung der BinärpräfixeIm Juni 1996 schlug die Internationale elektrotechnische Kommission (IEC) einen Standard für Binärpräfixe vor.[1][2] Dieser Vorschlag wurde im Dezember 1998 als Standard angenommen und im Januar 1999 als Ergänzung der Norm IEC 60027-2 veröffentlicht.[3] Er führte die Präfixe kibi, mebi, gibi, tebi, pebi und exbi für binäre Vielfache von Einheiten ein. In diesen Bezeichnungen wurden die ersten zwei Buchstaben der bereits standardisierten SI-Präfixe um „bi“ für „binär“ ergänzt. Für die Symbole der Binärpräfixe wurden die Symbole der SI-Präfixe verwendet und an diese der Kleinbuchstabe „i“ angehängt, wobei für das kibi im Gegensatz zum kilo der Großbuchstabe „K“ verwendet wurde. In dem Standard wurde außerdem darauf hingewiesen, dass die SI-Präfixe nur für auf Zehnerpotenzen basierende Vielfache verwendet werden sollten. Diese Ergänzungen wurden in die im November 2000 veröffentlichte zweite Auflage der Norm IEC 60027-2 integriert. In die im August 2005 veröffentlichte dritte Auflage der Norm IEC 60027-2 wurden auch die Binärpräfixe zebi und yobi aufgenommen.[4] Die Binärpräfixe werden inzwischen auch von anderen Standardisierungsorganisationen unterstützt (z. B. IEEE 1541, BIPM/CIPM, CENELEC[5], EN[6]). Die Binärpräfixe sind gemäß der folgenden Tabelle definiert:
Beispiel: 300 GB (Gigabyte) ≈ 279,4 GiB (Gibibyte). Verwendung von SI-Symbolen für auf Zweierpotenzen basierende VielfacheIn der Vergangenheit wurden mangels standardisierter Alternativen zur Bezeichnung von auf Zweierpotenzen basierenden Vielfachen häufig standardwidrig SI-Präfixe verwendet, die den gewünschten Zweierpotenzen am nächsten kamen. Es sollte dann aus der Kombination mit den Einheiten Bit oder Byte oder einem anderen Kontext hervorgehen, dass eine Zweierpotenz gemeint war. Während dies bei Speicherbausteinen, die üblicherweise nur in Größen von Zweierpotenzen hergestellt werden, wenig problematisch ist, führte dies beispielsweise bei der Angabe von Festplattenkapazitäten in GB oder Datenübertragungsraten in MB/s oder Mbit/s zu Zweifeln hinsichtlich der genauen Bedeutung. Zudem wird die Abweichung bei höherwertigen Präfixen immer größer, so dass sie oft nicht mehr vernachlässigbar ist. Das für die SI-Präfixe zuständige Internationale Büro für Maß und Gewicht (BIPM) rät von dieser nicht standardkonformen Verwendung der SI-Präfixe ausdrücklich ab und empfiehlt für die Bezeichnung von Zweierpotenzen die Binärpräfixe gemäß IEC 60027-2.[7] Trotzdem ist diese Bezeichnungsweise auch heute (2007) noch sehr weit verbreitet. Die Werte der SI-Präfixe und der nächstliegenden Zweierpotenzen sind in der folgenden Tabelle dargestellt:
Statt des SI-konformen Kleinbuchstabens „k“ wird auch der Großbuchstabe „K“ geschrieben (häufig nur als „kah“ gesprochen), um auf die beabsichtigte Abweichung von der Zehnerpotenz hinzuweisen. So kann „k“ für 1000 Einheiten verwendet werden und „K“ für 1024. Diese Konvention ist jedoch weder Bestandteil eines Standards, noch wird sie konsequent angewendet. Zudem kann dieser Ansatz nicht auf die größeren Präfixe übertragen werden. Verhältnis der binären und dezimalen Präfixe
Die Werte der SI-Präfixe steigen in Zehnerpotenzen, weswegen die SI-Präfixe auch als dezimale Präfixe bezeichnet werden, während die Werte der Binärpräfixe in Zweierpotenzen ansteigen. Konkret steigen die Werte der dezimalen Präfixe – ausgehend von kilo – jeweils um den Faktor 103 = 1000 und die Werte der binären Präfixe um den Faktor 210 = 1024. D. h. kilo entspricht 10001, mega 10002, giga 10003 usw., und kibi entspricht 10241, mebi 10242, gibi 10243 usw. Beschreibt Die folgende Tabelle gibt eine Übersicht über die sich daraus ergebenden Verhältnisse.
Ursachen und GeschichteEin wichtiger Bestandteil eines Computers ist der Arbeitsspeicher, der heute üblicherweise als Halbleiterspeicher realisiert wird. Die einzelnen Speicherzellen werden mit Hilfe von parallelen, binär arbeitenden Leitungen adressiert, die zusammengefasst als Adressbus bezeichnet werden. Mit einem Adressbus, der n Leitungen besitzt, können 2n Speicherzellen adressiert werden. Daher werden Halbleiterspeicher üblicherweise in Größen von Zweierpotenzen hergestellt. Mit zunehmender Größe der Speicher wurde es mangels standardisierter Alternativen üblich, SI-Präfixe mit den Speichereinheiten Bit und Byte zu verwenden, um Zweierpotenzen zu quantifizieren, obwohl die SI-Präfixe auf Zehnerpotenzen basieren. Bei Datenspeichern mit sequentieller Adressierung oder bei der sequentiellen Übertragung von Daten gibt es allerdings keinen Grund, mit Zweierpotenzen zu arbeiten, sodass hier die SI-Präfixe meist standardkonform verwendet werden. Dies hat zu einiger Verwirrung geführt, da manchmal nicht mehr eindeutig erkennbar ist, ob der jeweilige SI-Vorsatz standardkonform als Zehnerpotenz oder standardwidrig als Zweierpotenz interpretiert werden soll. Beispielsweise haben sich für die Bezeichnung „1 MB“ in der Praxis drei verschiedene Interpretationen eingebürgert:
Außerdem findet sich noch die Bezeichnung „1 Mb“ (mit kleinem „b“ für „Bit“):
Diese inkonsequente Vorgehensweise kann beim Rechnen mit Einheiten zu schwer nachvollziehbaren Fehlern führen, wie an folgendem einfachen Beispiel gezeigt werden soll: Ein Computerbenutzer will eine Datei mit der angegebenen Größe von „40 MB“ aus dem Internet herunterladen und hat dazu eine Datenleitung mit einer Datenübertragungsrate von 8 Mbit/s zur Verfügung. Die zur vollständigen Übertragung dieser Datei benötigte Zeit lässt sich mit der Umrechnung 1 B = 8 bit (vereinfacht) folgendermaßen berechnen: Hier drängt es sich auf, die „MB“ im Zähler gegen die „MB“ im Nenner zu kürzen, sodass sich leicht ein Ergebnis von Für eine saubere Lösung dieses Problems gibt es zwei Möglichkeiten:
Die Einführung der Binärpräfixe bedeutet nicht, dass sie die SI-Präfixe für die Verwendung mit Bits und Bytes ersetzen sollen. Beispielsweise kann man die Größe eines 536.870.912 Byte großen Arbeitsspeichers mit 536.870.912 B, 229 B, ca. 537 MB oder eben praktischerweise als 512 MiB angeben. Für die sehr weit verbreitete Angabe von Dateigrößen oder verfügbarem Festplattenspeicherplatz in Zweierpotenzen gibt es für die meisten Anwender keinen ersichtlichen Grund. Das Arbeiten mit Zweierpotenzen ist beispielsweise beim Addieren oder Subtrahieren von Datenmengen mit verschiedenen Binärpräfixen und beim Übergang auf größere oder kleinere Binärpräfixe ganz erheblich umständlicher als bei der Verwendung der auf das Dezimalsystem zugeschnittenen SI-Präfixe. Akzeptanz und VerbreitungZumindest bis zum Januar 2002 wurden die Binärpräfixe in industrieller und wissenschaftlicher Literatur sowie in Software wenig beachtet und somit nur selten verwendet.[8] Auch bis heute ist nur eine sehr langsam zunehmende Akzeptanz und Verbreitung festzustellen. Beispielsweise wird in den Informationen für Autoren des IEEE ausdrücklich auf die standardkonforme Verwendung von SI-Präfixen hingewiesen.[9] Das Computermagazin PC Games Hardware verwendet sie ab der Ausgabe 11/2007 (Erscheinungsdatum 2. Oktober 2007).[10] Ferner gibt es mittlerweile einige Programme, welche die Binärpräfixe unterstützen, z. B. der Linux-Kernel, die GNU core utilities[11], phpMyAdmin und einige Bittorrent-Programme. Quellen
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Binärpräfix aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





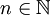 die Präfixe derart, dass
die Präfixe derart, dass 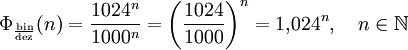
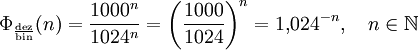
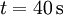 ergibt. Wenn jedoch mit dem „MB“ im Zähler eine Zweierpotenz gemeint ist, während im Nenner eine Zehnerpotenz gemeint ist, kann man diese Einheiten nicht gegeneinander kürzen, obwohl dies praktisch nicht mehr ersichtlich ist.
ergibt. Wenn jedoch mit dem „MB“ im Zähler eine Zweierpotenz gemeint ist, während im Nenner eine Zehnerpotenz gemeint ist, kann man diese Einheiten nicht gegeneinander kürzen, obwohl dies praktisch nicht mehr ersichtlich ist.


