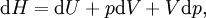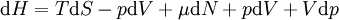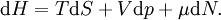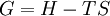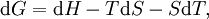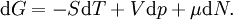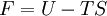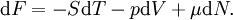Meine Merkliste

Charakteristische Funktion (Physik)

Die charakteristischen Funktionen bezeichnen in der Thermodynamik die totalen Differentiale und damit die Änderungen der thermodynamischen Potentiale: Innere Energie U, Enthalpie H, Helmholtz-Potential F und Freie Enthalpie G.

Die wichtigste charakteristische Funktion ist die aus dem Ersten Hauptsatz der Thermodynamik folgende Fundamentalgleichung

$\mathrm dU = T\mathrm dS - p\mathrm dV + \mu \mathrm{d}N. \!$

Aus den Definition der Enthalpie H

$H = U + pV \!$

folgt wegen $\mathrm d(pV) = p\mathrm dV + V\mathrm dp \!$ :

$\mathrm dH = \mathrm dU + p\mathrm dV + V\mathrm dp, \!$

und mit der Fundamentalgleichung erhält man

$\mathrm dH = T\mathrm dS - p\mathrm dV + \mu \mathrm{d}N + p\mathrm dV + V\mathrm dp \!$

und damit die charakteristische Funktion:

$\mathrm dH = T\mathrm dS + V\mathrm dp + \mu \mathrm{d}N. \!$

Aus der Definition der Freien Enthalpie G

$G = H - TS \!$

folgt

$\mathrm dG = \mathrm dH - T\mathrm dS - S\mathrm dT, \!$

und damit die charakteristische Funktion

$\mathrm dG = - S\mathrm dT + V\mathrm dp + \mu \mathrm{d}N. \!$

Zuletzt noch die Definition des Helmholtz-Potentials F

$F = U - TS \!$

folgt entsprechend

$\mathrm dF = -S\mathrm dT - p\mathrm dV + \mu \mathrm{d}N. \!$

Siehe auch: totales Differential

Dieser Artikel basiert auf dem Artikel Charakteristische_Funktion_(Physik) aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar.

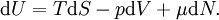
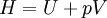
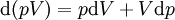Lesen Sie alles Wissenswerte über unser Fachportal chemie.de.

Erfahren Sie mehr über das Unternehmen LUMITOS und unser Team.

Erfahren Sie, wie LUMITOS Sie beim Online-Marketing unterstützt.

Die Fachportale von LUMITOS