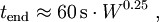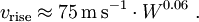Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Formelsammlung Kernwaffenexplosion
Die Formelsammlung Kernwaffenexplosion ist ein Teil der Formelsammlung, in der auch Formeln zu anderen Fachbereichen zu finden sind. Produkt-Highlight
Modell für Detonationswellen im homogenen LuftraumDer von der früheren US-Behörde Defense Nuclear Agency (DNA) entwickelte Standardkurve für die Druckwelle einer 1-Kilotonnen-Explosion liegt die folgende Beziehung zwischen dem Abstand R vom Explosionszentrum und dem Druckpegel OP zugrunde, wobei von einer Freiluftexplosion in einer homogenen unbegrenzten Atmosphäre unter Meeresniveaubedingungen (P = P0 = 101325 Pa und T = T0 = 288,15 K) ausgegangen wird:
Dabei ist R in m einzusetzen (der Übersichtlichkeit wegen wurde auf die Einheiten-Divisoren in der Formel verzichtet), und das Ergebnis ist OP in Pa. Der dynamische Druck ergibt sich aus wobei n das Dichteverhältnis vor und hinter der Stoßfront und P der Druck der ungestörten Atmosphäre ist. Für Luft ist κ ist der Adiabatenexponent, und der Index s deutet an. dass κ infolge der Stoßerhitzung hinter der Stoßfront nicht mehr den klassischen Wert für Luft von 1,402 besitzt, da durch Ionisation mehr Freiheitsgrade hinzukommen. Unterhalb von etwa 1000 kPa ist der Korrekturterm vernachlässigbar; für höhere Drucke Für werden zunächst einige temporäre Variablen benötigt, über die dann die Korrektur für κ resultiert: Dann ist Aus den hier berechneten Größen folgt auch der Normalreflexionsfaktor Fn, der die Druckerhöhung bei senkrechter Reflexion wiedergibt (trivialerweise 2 bei gewöhnlichen Schallwellen): Mit diesen Resultaten ergibt sich aus den Rankine-Hugoniot-Gleichungen die Ausbreitungsgeschwindigkeit und die Windgeschwindigkeit der Stoßfront: Daraus ergibt sich durch Integration der reziproken Geschwindigkeit auch die Laufzeit der Druckwelle zu einem bestimmten Radius. SkalierungsfaktorenDer wichtigste Skalierungsfaktor ist die Sprengkraft- oder Sachs-Skalierung. Die Standardkurven sind für 1 kT definiert; für beliebige Energien W (gleicher mechanischer Anteil vorausgesetzt) ist für beliebige Längen- und Zeitgrößen S die Gleichung anzuwenden. Dabei ist W bereits ein auf den typischen mechanischen Anteil von Atomwaffen (etwa 50 bis 60 Prozent der Gesamtenergie) normiert. Für andere als nukleare Explosionen muss um das Verhältnis der mechanischen Anteile ξ korrigiert werden. Nimmt man den Mittelwert 55% als Referenzwert für Nuklearexplosionen, so gilt für eine Explosion mit Energie E und mechanischem Anteil ξ Für chemische Explosionen kann näherungsweise ξ = 1 gesetzt werden. Für gegebenen Luftdruck P und Temperatur T gehen zudem in die korrigierte 1-kT-Druck- und Zeitkurve ein: Der Zeitskalierungsfaktor ist für die Laufzeit der Druckwelle von Bedeutung. Über Druck bzw. Temperatur wird auch die weiter unten benötigte Schallgeschwindigkeit skaliert. Sind Explosionszentrum und Ziel auf unterschiedlichen Höhen, so zeigen Beobachtungswerte und theoretische Rechnungen, dass für den Druck die Skalierungsfaktoren für die Höhe des Zieles statt des Explosionsherdes zu wählen sind. Für die Laufzeit sind die Verhältnisse komplizierter. Zusätzlich ist zu beachten, dass der mechanische Wirkungsgrad bei geringer Dichte kleiner wird. In etwa 30 km Höhe liegt er noch zwischen 30% und 40% (Glasstone, Dolan, The Effects of Nuclear Weapons,1977; kurz EoNW77), in größeren Höhen nimmt er dann rapide ab. Modell für Luftexplosion mit Reflexion
Das DNA-Modell beschreibt auch die Druckwelle bei Luftexplosionen, also unter Berücksichtigung der Reflexion an der Oberfläche. Bei der Berechnung sind zwei Regime zu unterscheiden, nämlich das Regime der regulären Reflexion und das der Mach-Reflexion. Für das erstere benötigt man neben dem oben berechneten Normalreflexionsfaktor Rn noch einige temporäre Variablen und Koeffizienten, um dann den Überdruck für reguläre Reflexion, OPreg berechnen zu können. Dabei wurde gelegentlich von Druckgrößen nur der Betrag verwendet (z.B. in Exponenten oder bei nicht-ganzzahliger Potenzierung usw.), der Übersichtlichkeit wegen aber auf zusätzliche Symbole verzichtet. HöhenkoeffizientenSeien H und GR für eine 1-kT-Explosion gegeben. Dann sind die Raumdiagonale R der Einfallswinkel α der Primärfront sowie einige temporäre Variablen wie folgt definiert: Grenzwinkel αM zwischen regulärer und Mach-Region und (Winkel-)Breite β der Zone, wo die Wellen verschmelzen, Hilfsvariablen und Schaltparameter σ: Reguläre ReflexionAusgangspunkt ist die DNA-Standardfunktion, die auf die Raumentfernung R angewendet wird und daraus Ein Speziallfall ist die Situation im Hypozentrum: Mach-ReflexionZunächst wieder ein paar Zwischenvariablen:
Nun setze 2^(-1/3)*GR anstelle von R in die DNA-Formel OP(R) ein und setze das daraus erhaltene Ergebnis OP1 hier ein: Der Abstand GRM, an dem die Verschmelzung von direkter und reflektierter Welle einsetzt, lässt sich auch annähern durch GesamtamplitudeDer Gesamt-Überdruck OPair ist dann Der dynamische Druck folgt dann mit dem Dichteverhältnis in der resultierenden Druckfront (anstelle der Standarddruckwelle) na=n(OPair): Die Berechnung der Ausbreitungsgeschwindigkeit der Welle kann nun mit OPair statt OPDNA geschehen; die Windgeschwindigkeit ws berechnet man sinnvollerweise aus DPair, weil dort die Restriktion auf die Horizontale bereits berücksichtigt worden ist: wobei ρ2 = n ρ0 die Dichte hinter der Stoßfront ist. Laufzeit der DruckwelleUm die Laufzeit der Druckwelle zu errechnen, ist die reziproke Geschwindigkeit der Stoßfront über die (auf die tatsächliche Sprengkraft skalierte) Entfernung zu integrieren. Bei Luftexplosionen sind hier zwei Wegabschnitte zu unterscheiden:
Das DNA-Modell verwendet einen Näherungsfit, der ohne rechenaufwendige Integration auskommt. Zunächst wird eine Laufzeitfunktion für eine 1-kT-Freiluftexplosion definiert: Für Freiluftexplosionen müssen jetzt nur R und tfree um die Kubikwurzel von W/kT skaliert werden. Für Luftexplosionen wird ein weiterer Korrekturfaktor benötigt: Nun wird in die Laufzeitformel einfach Rν=R/ν statt R eingesetzt und das Ergebnis mit W^(1/3) skaliert: Für von den Standardbedingungen stark abweichende Bedingungen können die obigen Skalierungsfaktoren auch für Luftexplosionen angewendet werden. Für große Detonationshöhen muss die numerische Integration mit anhand lokaler Längen- und Zeitskalierungen korrigierter Ausbreitungsgeschwindigkeit verwendet werden. Dauer der positiven DruckphaseAuch diese Formeln sind durchweg für 1 kT Sprengkraft gegeben und können wie die übrigen durch das Kubikwurzelgesetz skaliert werden. Wieder sind zunächst einige Hilfsgrößen zu definieren, zunächst eine Zeitskalierung: Dann ist die Dauer der 1-kT-Überdruckphase am Boden
aus der ein "Rohwert" für die Überdruckdauer bei Luftexplosionen gewonnen wird, wobei Für beliebige Explosionshöhen für 1 kT Energie ist dann Obige Formeln gelten für den Überdruck. Die Dauer der positiven dynamischen Druckphase ist infolge der Massenträgheit der Luft in der Regel etwas länger als die der Überdruckphase Dauer des dynamischen DruckstoßesFür die folgende Berechnung der dynamischen Druckdauer sollte der GR den Wert nicht unterschreiten. und
sowie und mit
Die auf 1 kT skalierte dynamische positive Phasendauer ist dann Nützliche VereinfachungenIm Falle einer Explosion direkt am Boden vereinfacht sich die Beziehung für die Reflexion dergestalt, dass die halbkugelförmige Druckwelle sich wie eine Freiluftexplosion doppelter Sprengkraft verhält. In diesem Fall ist also Die Entfernung von der Bodenexplosion, in der ein bestimmter Druck OP angenommen wird, kann alternativ zum numerischen Lösen näherungsweise auch durch folgenden Fit bestimmt werden: Diese Näherung für eine 1-kT-Explosion ist – in Bezug auf das Originalmodell – zwischen 0,3 und 10000 PSI (2,1 und 69000 kPa) auf ±1% genau. Allerdings gilt diese Rechnung nur für einen Reflexionsgrad von 100%. Kernwaffentests in Nevada und im Pazifik zeigten einen Reflexionsgrad von nur etwa 70% für Wüstensand oder weichen feuchten Untergrund. Statt des doppelten ist hier also der 1,7-fache Wert der Freiluftsprengkraft einzusetzen. Der Radius verringert sich gemäß der Kubikwurzelregel. Für Luftdetonationen über Stadtgebieten, wo die Druckwelle Energie durch Zerstörungsarbeit verliert, gilt vermutlich etwas Ähnliches. Jedoch sind genaue Daten hierzu bisher nicht veröffentlicht worden. Die Explosionshöhe, bei der der Grundradius GROP für einen bestimmten Druck OP maximal wird, ist näherungsweise gegeben durch die Beziehung: Der durch diese Wahl von HOP maximierte Radius GROP ist dann ungefähr Diese Formeln sind in Bezug auf das Originalmodell auf ±20% für H und ±10% für GR im Bereich von 0,1 bis 10000 PSI (0,69 bis 69000 kPa) jedoch unter Vernachlässigung der atmosphärischen Druckvariation und für ebenes Gelände). Die Näherung ist allerdings ein Kompromiss zwischen dem BLAST-Modell und Daten aus EoNW77. Die Abweichungen vom BLAST-Modell resultieren überwiegend aus den Abweichungen beider Quelldaten. Grenzen des ModellsGrenzen für EingabewerteDas DNA-Modell ist in weiten Bereichen von Radius und Druck gültig. Räumliche Modellgrenzen skalieren wie alle übrigen Längenskalen mit der Kubikwurzel der Sprengkraft.
Dabei ist LM = 20 SL W1/3, falls H < 25 SL W1/3 und 0 sonst, sowie LQ = max(GRM,80 m). Die Modellgrenzen für die statische Überdruckphasendauer sind die gleichen wie für den statischen Überdruck selbst. Diese Grenzen sind recht konservativ gewählt; plausible Ergebnisse liefert das Modell, mit Ausnahme der dynamischen Phasendauer, noch in mehr als dem Doppelten der oberen Radiusgrenze, wenn nahezu ideale Bedingungen vorausgesetzt werden. Die W-Skalierung beispielsweise ist theoretisch unbegrenzt und exakt gültig; die Grenzen ergeben sich vor allem aus dem Druckgradienten der Atmosphäre und den spezifischen Eigenschaften von Atomwaffen, auf die sich das Modell ursprünglich bezieht. GenauigkeitDie Genauigkeit des Modells hängt stark von der Genauigkeit der Messwerte zusammen, für die keine Angaben verfügbar sind. Abweichungen in Folge von nicht vorhersagbaren Umwelteinflüssen (Geländeformation, Winde, lokale Temperaturschwankungen usw.) sowie Unsicherheit bei der gemessenen Sprengkraft führen zu teilweise erheblichen Fehlern. Für große Distanzen können Reflexion und Refraktion zu lokaler Bündelung von Wellenfronten und damit zu erheblich größeren Druckspitzen führen. Daher wird zudem der zumeist erheblich geringere Fehler zu komplexen numerischen Modellen oder den theoretischen Werten (bei Näherungsformeln) mit angegeben.
BeispielDie wahrscheinliche Explosion eines Meteoroiden beim Tunguska-Ereignis lässt sich näherungsweise durch eine Explosion von etwa 15 MT TNT-Äquivalent in ca. 8 km Höhe darstellen. Für solch eine Explosion liefert obiges Modell einen Überdruck von 101 kPa (knapp 1 atm) im Hypozentrum, 35 kPa im Umkreis von 16 km (hier treten schwerste Verwüstungen auf, was sich mit den Beobachtungen deckt). Orkanartige Winde über 11 Bft treten im Umkreis von 30 km auf und lassen noch einzelne Bäume umstürzen. In 65 km Grundradius beträgt der Druck noch mehr als 4 kPa, wodurch Fenster und Türen eingedruckt und Dächer beschädigt werden. Der Windstoß im Freien beträgt in diesem Abstand nicht mehr als 10 m/s (5 Bft), jedoch kann an Öffnungen (Türen, Fenster) der Überdruck zu kurzzeitigen Strömungen von bis zu 69 m/s führen und Personen umwerfen. Dies deckt sich mit beobachteten Schäden und Zeugenaussagen in der Stadt Wanawara, die 65 km vom vermuteten Hypozentrum entfernt liegt. Dort traf die Druckwelle dem DNA-Modell zufolge nach knapp drei Minuten ein (175 sek Fit, 176 sek integriert; Standardatmosphäre 1976). Feuerballentwicklung bei KernexplosionenAusdehnung
Eng mit der Druckwellenausbreitung hängt auch die Ausbildung des Feuerballs einer Kernwaffenexplosion zusammen. Im Wesentlichen gibt es drei Hauptphasen, die im genannten Artikel beschrieben werden:
In dichten Atmosphärenschichten (unter 30 Kilometer Höhe) ist die Dauer und die räumliche Ausdehnung der ersten Phase gegenüber den nachfolgenden Phasen vernachlässigbar. Die folgenden können daher annähernd unabhängig von der ersten beschrieben werden. Die folgenden Formeln sind gültig für Höhen unter 30 km, wo die mittlere freie Weglänge für die primären Röntgenstrahlen klein gegenüber dem skalierten Feuerballdurchmesser sind und ein Feuerball somit auf ähnliche Weise entstehen kann, wie auf Meeresniveau. Generell sind diese Formeln nur Näherungen, die mit entsprechender Vorsicht zu verwenden sind. Das Wachstum des Feuerballs in der 2. Phase skaliert mit der Explosionsenergie in der gleichen Weise wie die Druckwelle selbst (Bezeichnungen siehe oben): Um die mit Umgebungsbedingungen und Sprengkraft sowie Sprengkopftyp (geringfügig) unterschiedlichen Energieanteile von Druckwelle ξb und Wärme ξh (letztere ist für die Ausdehnung des späten Feuerballs maßgeblich) zu berücksichtigen, werden mechanische ("blast") und thermische ("heat") Sprengkraft, Wb und Wh unterschieden: Bei einer Explosion im Kilotonnenbereich sind die Anteile etwa ξh = 50% und ξh = 35% und somit Wb = Wh = W. Aus in der Literatur vorhandenen Diagrammen ist folgende Näherungsformel für eine 20-kT-Luftexplosion gewonnen worden, die die Grundlage für die obige Abbildung ist (man beachte, dass dort der Durchmesser D = 2R angegeben ist): t ist dabei der Betrag der Zeit nach der Zündung in Sekunden und wird als dimensionslose Zahl verwendet. Der späte Feuerballdurchmesser (3. Phase) R∞ skaliert mit W0,39 statt mit der Kubikwurzel, so dass sich für die W-Skalierung ergibt: Dabei W wieder in Einheiten von kT TNT-Äquivalent, ferner ist R0 ein auf 1 Sekunde nach dem tC-Gesetz extrapolierte (imaginärer, rein rechnerischer) Radius, R∞, sowie S0 und S∞ Skalierungsfaktoren für Umgebungsdruck und -temperatur (auf oder nahe Meeresniveau können sie auf 1 gesetzt werden). S0 ist einfach zu berechnen, da nur die Längen- und Zeit-Skalierungsfaktoren für die Druckwelle (auch für das Zeitargument t) eingehen: S∞ ist weniger offensichtlich, da auch die optische Dicke τ eine wichtige Rolle spielt. Eine erste Näherung berücksichtigt nur die Zunahme des Radius mit abnehmendem Druck: Die effektive optische Dicke, die für den gegenüber 1/3 etwas größeren Exponenten von W verantwortlich ist, nimmt jedoch mit abnehmendem Druck (geringere Luftdichte) sowie der damit zunehmenden Ausdehnungszeit (Feuerball hat mehr Zeit zum Abstrahlen) ab. Mit der Beziehung
der relativen Dichte Sρ=ρ/ρ0 und ergibt sich Die Temperatur hat demnach nur geringen Einfluss auf den Endradius. Eine vernünftige Näherung ist somit Im Fall von Bodenexplosionen ist nur Wb aufgrund von Reflexion zu verdoppeln; wegen der Absorption von ungefähr der Hälfte der Wärme am Boden kann für Wh am Boden der gleiche Wert wie für Luftexplosionen eingesetzt werden. HelligkeitFür die theoretische Effektivtemperatur (d.h. die einem Planck-Strahler gleicher Strahlkraft entsprechende Temperatur) Tthedes Feuerballs einer 20-kT-Explosion wurde aus Abb. 2.123 aus EoNW77 eine zusammengesetzte Näherungsfunktion gewonnen: wobei τ = log10 t und Die gemessene Effektivtemperatur Tobs in der Frühphase ist deutlich geringer, was auf Absorption durch ionisierte Luftgase zurückgeführt werden kann. In diesem Fall wird mit Die Koeffizienten sind
Die Leuchtkraft ergibt sich dann aus dem Stefan-Boltzmann-Gesetz:
wobei σ = 5.6704·10-8 W m-2 K-4 die Stefan-Boltzmann-Konstante ist. Nach Beobachtungen wird etwa 1% der thermischen Energie im ersten "Peak" freigesetzt. Dieses entspricht jedoch einer Temperaturfunktion, die zwischen beiden obigen Funktionen liegt. Ein sinnvoller Kompromiss ist offenbar
Ferner deuten andere Daten auf einen geringfügig (ca. 20%) langsameren Verlauf der Explosion im zweiten Peak hin, was durch die Korrektur unter Erhaltung der abgestrahlten Energie erreicht wird. Ursache für diese Diskrepanz sind vermutlich Ungenauigkeiten in den publizierten Daten. Für die Abbildung wurde die unkorrigierte (und damit der Originalabbildung am ehesten entsprechende) Funktion verwendet. Die zeitliche Entwicklung der Helligkeit zu Beginn des zweiten thermischen Impulses skaliert anders als die räumliche Ausdehnung. Nach EoNW77 ist die zeitliche Skalierung gegeben durch Die Leuchtkraft (Strahlleistung) L skaliert mit Der Feuerball wird also heller mit zunehmender Höhe (also abnehmender Luftdichte), leuchtet dafür aber kürzer. Feuerball-SkalierungsregelnAus den Skalierungsregeln der Druckwelle für Explosionsenergie und Umgebungsdruck sowie denen aus EoNW77 für die Zeitentwicklung der Leuchtkraft lässt sich ein Ähnlichkeitsparameter f ableiten, indem beide Skalierungsregeln gleichgesetzt werden: Für den ungefähren Bereich 1 ≤ f ≤ 20000 gilt dann für Zeit- und Längenskalierung Für sehr kleine f<1 nimmt die thermische Emissionszeit weiter ab, während der Enddurchmesser zunehmend von der Druckwelle bestimmt wird und daher mit (Y/SP)1/3 oder geringfügig flacher skaliert (siehe Unterabschnitt zum Feuerballwachstum für eine Kompromisslösung). Bei sehr großen f>20000 geht die optische Dicke der die Feuerblase verhüllenden Stoßfront gegen unendlich und verschwindet erst unterhalb einer bestimmten Temperatur, dann jedoch schlagartig. Größere Feuerballdurchmesser ändern daran nichts mehr, so dass auch hier eine (Y/SP)1/3-Skalierung, jedoch für Radius und Leuchtdauer zu erwarten ist. Für diese Bereiche liegen jedoch keine Messwerte vor, so dass dies nur grobe Schätzungen sind. Ferner ist die f-Charakterisierung nur gültig, solange die mittlere freie Weglänge der direkten Röntgenstrahlung aus dem Explosionszentrum klein gegenüber dem Feuerballdurchmesser ist (das ist oberhalb von etwa 30 km nicht mehr gegeben), sowie der Feuerballradius kleiner als die Skalenhöhe der Atmosphäre ist. Bei Umrechnungen auf die Atmosphäre eines anderen Planeten (z.B. zur Modellierung des Shoemaker-Levy 9-Einschlags auf Jupiter) ist zudem deren unterschiedliche Zusammensetzung zu berücksichtigen. Feuerbälle mit f=1 können mit der abgebildeten Zeit-Temperatur-Kurve berechnet werden, wobei die Zeit und der Durchmesser mit (Y/SP)1/3 und die Temperatur mit SP1/4 skaliert wird. Letzteres bedeutet anschaulich: Bei 1/8 des Meerenhöhendrucks dehnt sich der skalengleiche Feuerball doppelt so weit aus wie in Meereshöhe bei simpler Kubikwurzelskalierung bei gleicher Energie, und er braucht dafür doppelt so lange. Die Energie wird daher über die vierfache Fläche halb so schnell freigesetzt, also mit 1/8 der Intensität. Die Intensität skaliert bei konstantem f also linear mit dem Druck. Aus dem Stefan-Boltzmann-Gesetz folgt dann die Skalierung der Temperatur. Größe und Form der PilzwolkeDie Entwicklung der Pilzwolke hängt stark von den Wetterbedingungen ab. Dennoch ist es möglich, für durchschnittliche Bedingungen und annähernd Windstille eine Näherung zu beschreiben. Für kleine Wh (bis ca. 10 kT) gilt für Endhöhe H und -breite B der Pilzwolke Für größere Energien wird die Form der Wolke stark von der atmosphärischen Schichtung (v.a. der Tropopause) beeinflusst. Der Aufstieg wird gehemmt, während die Wolke sich stärker in die Breite ausdehnt. Die folgende Formel ist eine Anpassung an die Abbildung 2.16 aus EoNW77.
wobei LW = log10(W/kT). Der stetige Übergang beider Näherungen wird durch eine Interpolation unterhalb von etwa LW = 1.5 bzw. Wh = 30 kT ermöglicht. Die Zeit bis zum Erreichen der Endhöhe kann für Wh < 1 MT grob abgeschätzt werden durch die Beziehung die Steigrate durch (Quelle: Daten aus EoNW64, PDF bei Trinity Atomic Web Site als Grundlage für Potenzgesetz-Abschätzung.) Siehe auch
|
|||||||||||||||||||||||||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Formelsammlung_Kernwaffenexplosion aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |




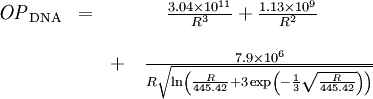
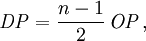
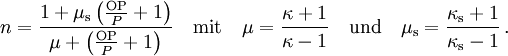
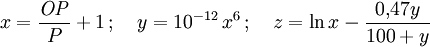
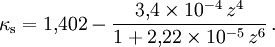
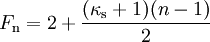
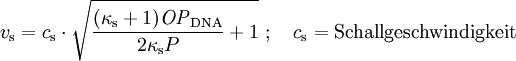
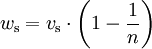
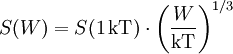
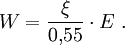

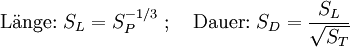
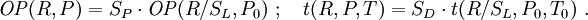
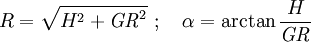
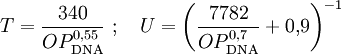
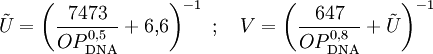
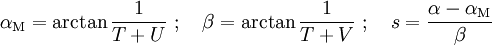
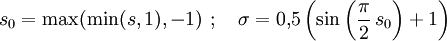
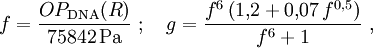
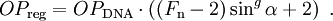
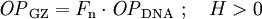
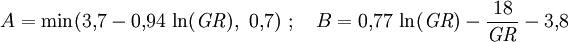
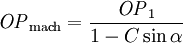
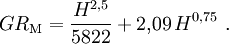
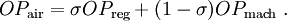
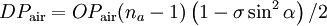
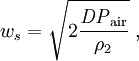
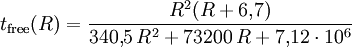
![\nu=\left\{\begin{matrix}1&\mbox{wenn}\ GR\le GR_\mathrm{M}\\ \sqrt[3]{2}+\left(1-\sqrt[3]{2}\right)\frac{GR_\mathrm{M}}{GR}&\mbox{sonst} \end{matrix}\right.](images/math/7/f/2/7f27cc1ef4e4c31ee2b7ea323d95f33f.png)
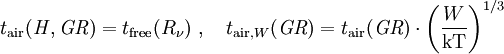
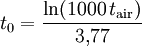
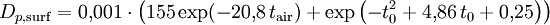 ,
,
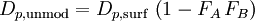
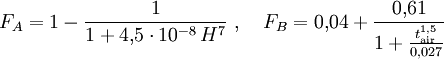
![D_p=D_{p,\mathrm{unmod}} \left(1{,}16\,\exp\left(-\left[\frac{\frac{H}{0{,}3048}-156}{1062} \right]\right)\right)](images/math/6/d/9/6d97301be44c14372a7eb89929b61c69.png)
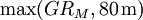
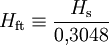
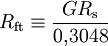 ,
,
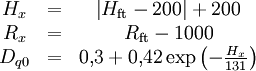
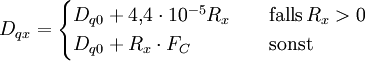
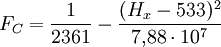 .
.
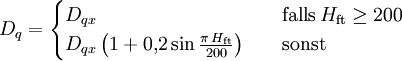
![\mathit{OP}(r)=\mathit{OP}_\mathrm{DNA}(r/\sqrt[3]{2})\ .](images/math/d/c/3/dc30b8e2841d521f19bb44c984ada4ba.png)
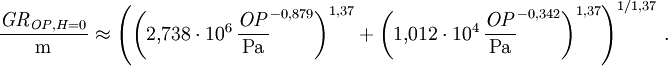
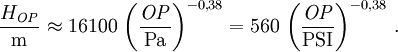
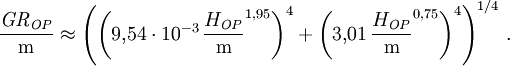
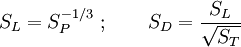
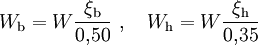
![R(t)=\left[\left(R_{-4} t^C\right)^{-3}+R_\infty^{-3}\right]^{-1/3}\ ;\quad R_{-4}=13\,\mathrm{m}\ ;\ R_\infty=236\,\mathrm{m}\ ;\ C=0{,}406\ .](images/math/d/4/a/d4a484871ef2243337a89db1691e63f9.png)
![R(t,W)=\left[\left(S_0 W_\mathrm{b}^{(1-C)/3}R_0 t^C\right)^{-3}+\left(S_\infty W_\mathrm{h}^{0{,}39}R_\infty\right)^{-3}\right]^{-1/3}\ ,](images/math/7/2/2/722bd63b2f7cc4ffe8021129f8bb6f2a.png)

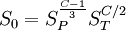
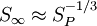
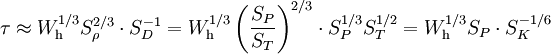
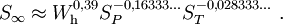
![R(t,W)=\left[\left(\left[\frac{W_\mathrm{b}}{S_P}\right]^{0{,}198}S_T^{0{,}203}R_0 t^{0{,}406}\right)^{-3}+\left(W_\mathrm{h}^{0{,}39}S_P^{-0{,}2}R_\infty\right)^{-3}\right]^{-1/3}\ .](images/math/9/4/a/94aeb47ba294abcae246deedb52ef129.png)
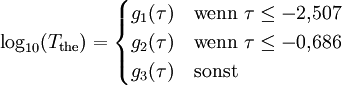
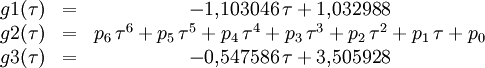
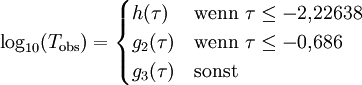
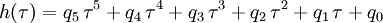
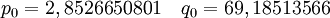
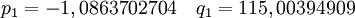
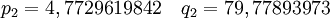
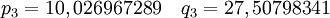
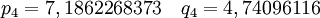
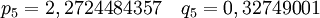
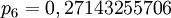
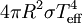 ,
,
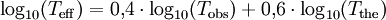 .
.
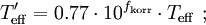
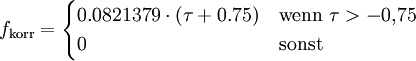
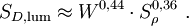
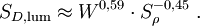
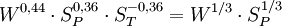
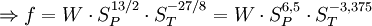
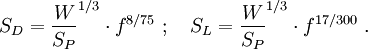
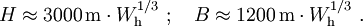
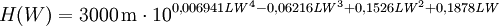 ,
,
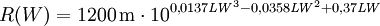 ,
,