Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Heisenbergsche UnschärferelationDie heisenbergsche Unschärferelation oder Unbestimmtheitsrelation ist die Aussage der Quantenphysik, dass jeweils zwei Messgrößen eines Teilchens (etwa sein Ort und Impuls) nicht gleichzeitig beliebig genau bestimmt sind. Sie ist nicht die Folge von Unzulänglichkeiten eines entsprechenden Messvorgangs, sondern prinzipieller Natur. Die Unschärferelation wurde 1927 von Werner Heisenberg im Rahmen der Quantenmechanik formuliert. Unter dem Begriff der Unschärfe ist mathematisch gesehen die sogenannte Standardabweichung gemeint. Der Begriff „Unbestimmtheitsrelation“ beschreibt die Aussage besser, da es nicht um die Genauigkeit in der Messung geht, sondern um die prinzipielle Unmöglichkeit. Produkt-Highlight
ÜberblickDie Unschärferelation bezüglich Ort und Impuls lässt sich als unmittelbare Konsequenz der Wellennatur der Materie in der Quantenphysik interpretieren. Sie wird oft irrtümlich damit erklärt, dass eine Messung des Ortes eines Teilchens notwendigerweise seinen Impuls stört. Heisenberg selbst hatte diese Erklärung zuerst gegeben. Die Unbestimmtheitsrelation gilt jedoch sogar dann, wenn nach der Messung des Ortes die Messung des Impulses an einer Kopie des Systems erfolgt (siehe: Die Ensemble-Interpretation). Ähnliche Unschärfebeziehungen gibt es auch zwischen anderen Paaren komplementärer Größen. Zwischen Energie und Zeit besteht ebenfalls eine Unschärfebeziehung, die aber von anderer Natur ist (siehe Energie-Zeit-Unschärferelation). Folgende Analogie verdeutlicht die Unbestimmtheit: Nehmen wir an, dass wir ein zeitveränderliches Signal, zum Beispiel eine Schallwelle, haben und wir die genaue Frequenz dieses Signals zu einem bestimmten Zeitpunkt messen wollen. Das ist unmöglich, denn um die Frequenz exakt zu ermitteln, müssen wir das Signal über eine gewisse Zeitspanne beobachten, und dadurch verlieren wir Zeitpräzision. Das heißt, ein Ton kann nicht innerhalb nur einer beliebig kurzen Zeitspanne da sein, wie etwa ein kurzer Impuls, und gleichzeitig eine exakte Frequenz besitzen, wie sie etwa ein ununterbrochener reiner Ton hat. Die Zeitdauer und die Frequenz der Welle sind analog zu betrachten zum Ort und Impuls eines Teilchens. Die Unbestimmtheitsrelation wird oft verwechselt mit einem anderen quantenmechanischen Phänomen, dem Kollaps der Wellenfunktion, nach dem die Wellenfunktion, die ein Teilchen beschreibt, genau dann zerstört wird, wenn der Ort dieses Teilchens zu einem beliebigen Zeitpunkt bestimmt wird. Dieses Phänomen und die Unbestimmtheitsrelation sind verschieden, aber miteinander verwandt. Im Rahmen des mathematischen Formalismus ergeben sich die Wahrscheinlichkeitsverteilungen für Orts- und Impulsmessungen und damit die Unschärfen aus den zugehörigen Wellenfunktionen. Die Unschärferelation folgt dann aus dem Umstand, dass die Wellenfunktionen bezüglich Ort und Impuls über eine Fouriertransformation miteinander verknüpft sind. Die Fouriertransformierte eines lokal begrenzten Wellenpakets ist nun wiederum ein Wellenpaket, wobei das Produkt der Paketbreiten einer Beziehung gehorcht, die der obigen Unschärferelation entspricht. GleichungenDie Unschärferelation bezüglich Ort und Impuls ist der bekannteste Vertreter einer Gruppe von Unschärfebeziehungen, die ein grundlegendes Prinzip der modernen Physik darstellen. Gemäß dieser Beziehung gilt für die Unschärfe Δx des Ortes x und die Unschärfe Δp des Impulses p bezüglich der gleichen Richtung im Raum stets wobei
Die Interpretation einer Zeitunschärfe ist dabei etwas komplizierter als die einer Orts- oder Impulsunschärfe, da die Zeit ein Parameter und kein Operator ist. Die obige Formel gilt, wenn man als Δt den Zeitraum ansetzt, innerhalb dessen sich die Energie E des Teilchens im Mittel um ΔE ändert. Zustände des Teilchens, in denen sich die Energie stark ändern kann (z. B. Anregung durch Licht und Übergang in den Grundzustand), werden also nur kurzlebig sein (kleines Δt), und umgekehrt. In der Akustik der klassischen Physik existiert eine ähnlich aussehende Unschärferelation zwischen Frequenz und Zeit, die aber mit der heisenbergschen Unschärferelation direkt nichts zu tun hat. Für überlagerte Schallwellen, deren Frequenzunterschied Δf ist, gilt
Da die Unschärfe aus mathematischer Sicht die Standardabweichung ist, wird häufig auch σA statt ΔA geschrieben. InterpretationenDie heisenbergsche Unschärferelation wird verschieden interpretiert. Man unterscheidet die Ensemble-Interpretation, die eine Aussage über ein ganzes System macht, ein sogenanntes Ensemble, und die Kopenhagener Deutung, die ein einzelnes Teilchen beschreibt. Die Ensemble-InterpretationDer große Unterschied zu den bisherigen beiden Interpretationen ist, dass die Ensemble-Interpretation nicht wie bei Bohr oder Heisenberg Aussagen für ein Teilchen macht, sondern Wahrscheinlichkeitsaussagen für eine große Anzahl von Versuchsdurchgängen; allerdings mit – das ist die Voraussetzung – identischen Teilchen. Ein „Ensemble“ ist die Gesamtheit aller identischen Teilchen, die ein Präparationsverfahren ergibt. Sie dürfen in dem Experiment allerdings nicht miteinander wechselwirken, analog zu Photonen im Doppelspaltexperiment. Aussagen über ein Experiment sind in folgender Weise möglich: Das Ensemble wird halbiert, um an einem Teil des Ensembles eine Eigenschaft zu messen, etwa den Ort x, und an dem anderen Teil des Ensembles eine andere Eigenschaft zu messen, etwa den Querimpuls px. Mit den vielen Messwerten einer Eigenschaft, die man erhält, kann man nun Statistik betreiben. Man kann den Mittelwert der Messwerte bestimmen und auch die Standardabweichung, die als Größe für die mittlere Abweichung zu verstehen ist und auf dem Mittelwert aufbaut. Die Standardabweichung der Orte wird dann als Δx dargestellt. Dadurch kann die heisenbergsche Unschärferelation folgendermaßen formuliert werden: Es ist nicht möglich, ein Ensemble in einem Zustand so zu präparieren, dass für das ganze Ensemble erfüllt ist. Das Interessante an der Ensemble-Interpretation ist, dass mit dieser Interpretation die heisenbergsche Unschärferelation klar formuliert ist. Außerdem wird diese Interpretation wissenschaftlich anerkannt und gilt als Minimaltheorie, der die meisten Wissenschaftler zustimmen können. Zudem gelingt eine Verbindung von Theorie und Experiment. Schließlich sind Δx und Δpx klar und relativ einfach über die Standardabweichung definiert. Die Kopenhagener DeutungDie Kopenhagener Deutung war die erste abgeschlossene und in sich konsistente Interpretation des mathematischen Gebäudes der Quantenmechanik. Sie führte zu stärkeren philosophischen Diskussionen. Das Grundkonzept baut auf folgenden drei Prinzipien auf: Unverzichtbarkeit klassischer Begriffe: Klassische Begriffe werden in ihrer üblichen Bedeutung auch in der Quantenwelt benutzt, sie erhalten allerdings Vorschriften über ihre Anwendbarkeit. Das sind die Definitionsgrenzen von Ort und Impuls, unterhalb derer die Begriffe Ort und Impuls keinen Sinn mehr ergeben, also undefiniert sind. Die klassische Physik ist dadurch ausgezeichnet, dass gleichzeitig die raumzeitliche Darstellung, also die Möglichkeit der Ortsangabe zu gewissen Zeiten, und die Erhaltung des Kausalitätsprinzips, also die Bestimmung des zeitlichen Verlaufs bei Angabe eines Anfangszustandes, erfüllt sind. Komplementarität: In Bereichen, in denen die so genannte Wirkung in Größenordnung des planckschen Wirkungsquantums h, liegt, kommt es zu Quanteneffekten und zwar aufgrund unkontrollierbarer Wechselwirkungen zwischen Objekt und Messgerät. Komplementarität bedeutet nun, dass Raumzeitdarstellung und Kausalitätsforderung nicht beide gleichzeitig erfüllt sein können. Ansonsten würde sich folgender Widerspruch ergeben: Eine Eigenschaft eines Teilchens sei bestimmt. Dann muss nach der Quantenmechanik die Beeinflussung durch ein Messgerät fehlen, also muss eine Messung fehlen und damit geht der Sinn der Bestimmtheit verloren. Ganzheitlichkeit der Quantenphänomene: Die Vorstellung, dass ein Quantenexperiment ein völlig neues Phänomen aufweisen könnte, wenn das Experiment geändert wird, wenn zum Beispiel weitere Messung vorgenommen werden soll. Beim Doppelspaltexperiment findet beispielsweise gleichzeitig zur Impulsbestimmung noch eine Ortsbestimmung hinter einem Spalt statt. Niels Bohr und Werner Heisenberg, die beide die wesentlichen Begründer der Kopenhagener Interpretation, vertraten relativ ähnliche Ansichten, unterschieden sich jedoch in einem Punkt bei der Interpretation:
HerleitungIm Allgemeinen bestehen Unschärfebeziehungen auch zwischen Drehimpuls und Winkel, Phase und Teilchenzahl und zwischen vielen anderen Paaren von physikalischen Größen. Mit den Rechenmethoden der Quantenmechanik kann man für zwei Observablen A und B allgemein formulieren, mit Hierbei sind Diese Ungleichung sagt aus, dass das Produkt der A-Unschärfe und der B-Unschärfe mindestens halb so groß wie der Betrag des Erwartungswertes des Kommutators von A und B ist. Im Allgemeinen ist also die Mindestgröße des Unschärfeproduktes vom quantenmechanischen Zustand abhängig. Wie man sieht kann damit das Produkt der Unschärfen durchaus den Wert Null annehmen, und zwar genau dann, wenn die Observablen A und B miteinander vertauschen. In diesem Fall sind die Observablen gleichzeitig scharf messbar, es handelt sich um so genannte kompatible oder verträgliche Observablen. Die quadratische Standardabweichung
Dies ist bereits die Unschärferelation, welche aber noch in die gebräuchliche Form umgeformt werden muss. Eine komplexe Zahl z hat die Eigenschaft
wobei Re der Realteil und Im der Imaginärteil von z ist. Mit Für die Größe
Auf die selbe Weise erhält man
Damit wird die Differenz aus der Ungleichung zu
also gerade dem Kommutator. Damit erhält die Unschärferelation ihre bekannte Form BeispieleDie minimale Breite einer Tunnelbarriere kann über die Unschärferelation abgeschätzt werden. Betrachtet man ein Elektron mit der Masse me, welches eine Potentialdifferenz U durchtunnelt, so ergibt sich für die Ortsunschärfe und somit die minimale Breite der Tunnelbarriere
Bei einer Potentialdifferenz von 100 mV, wie sie etwa bei der Rastertunnelmikroskopie vorkommt, ergibt sich aufgrund dieser Beziehung eine kleinste Tunnelbarriere von etwa 0,3 nm, was sich gut mit experimentellen Beobachtungen deckt. Siehe auch
Literatur
|
|
| Dieser Artikel basiert auf dem Artikel Heisenbergsche_Unschärferelation aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





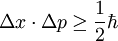
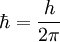 ,
, 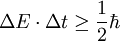 .
.
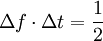 .
.
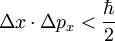
![\sigma_A^2 \sigma_B^2 \ge \left(\frac{1}{2 i} \langle [\hat{A},\hat{B}] \rangle_\psi \right)^2](images/math/d/9/1/d914d2dda3ab53ce3a3736818dea404f.png)
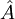 und
und 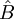 die den Observablen zugehörigen linearen, hermiteschen Operatoren. Der Ausdruck
die den Observablen zugehörigen linearen, hermiteschen Operatoren. Der Ausdruck ![[\hat{A}, \hat{B}]](images/math/c/0/8/c081d8bf21108f8283f018b863a75393.png) bezeichnet den Kommutator von
bezeichnet den Kommutator von 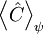 ist der Erwartungswert des Operators
ist der Erwartungswert des Operators 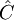 zum
zum 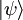 .
.
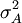 einer Observablen
einer Observablen 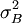 und
und 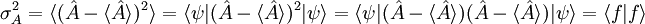
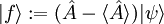 .
.
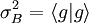
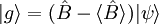 .
.
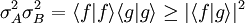
![|z|^2 = \mathrm{Re}(z)^2 + \mathrm{Im}(z)^2 \ge \mathrm{Im}(z)^2 = \left[\frac{1}{2 i}(z-z^*)\right ]^2](images/math/d/0/a/d0a5b50c85312571d7f2d29ce0fe0bc7.png) ,
,
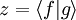 ergibt sich
ergibt sich
![\sigma_A^2 \sigma_B^2 \ge \left[\frac{1}{2 i}(\langle f|g\rangle - \langle g|f\rangle)\right ]^2](images/math/c/a/3/ca336ec1d2328d6072563e8f18f5a5bc.png)
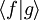 gilt
gilt
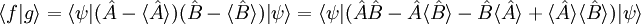
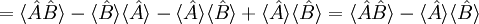 .
.
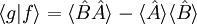 .
.
![\langle f|g\rangle - \langle g|f\rangle = \langle \hat A \hat B \rangle - \langle \hat B \hat A \rangle = \langle [\hat A , \hat B] \rangle_\psi\quad](images/math/f/e/7/fe71206ef6c8e894dc08e6c710a33b14.png) ,
,
![\sigma_A^2 \sigma_B^2 \ge \left[\frac{1}{2 i}\langle [\hat A , \hat B] \rangle_\psi \right ]^2](images/math/c/f/9/cf93b662cd0dc634f05be3c3901f11f5.png)
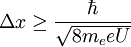 .
.


