Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Ideales FermigasAls ideales Fermigas bezeichnet man ein System aus nicht-wechselwirkenden Fermionen, also z.B. einem System aus nicht-wechselwirkenden Elektronen. Die Vernachlässigung sämtlicher Wechselwirkungen stellt in den meisten Fällen eine starke Vereinfachung dar, erlaubt jedoch in vielen Grenzfällen (z.B. niedrige Temperaturen) physikalisch korrekte Voraussagen. Produkt-HighlightMathematische BeschreibungIm Rahmen der statistischen Physik folgt mit Hilfe des großkanonischen Ensembles für die mittlere Besetzungszahl < ni > des Zustands Hierbei ist μ das chemische Potenzial, T die Temperatur und kB die Boltzmannkonstante. Da Fermionen dem Pauli-Prinzip unterliegen, kann ein Zustand maximal einfach besetzt sein, d.h. Entartetes FermigasIm Grenzfall niedriger Temperaturen nennt man das Gas entartetes Fermigas, da hier quantenmechanische Effekte besonders stark zur Geltung kommen. Z.B. zeigt sich, dass bei einer Temperatur von Null Kelvin das Fermigas einen endlichen Druck besitzt, den sogenannten Entartungsdruck. Dieser ist rein quantenmechanischer Natur und eine Folge des Pauli-Prinzips. BeispieleFolgende physikalische Systeme lassen sich wenigstens in erster Näherung durch ein ideales Fermigas beschreiben:
|
| Dieser Artikel basiert auf dem Artikel Ideales_Fermigas aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





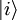 mit der Energie
mit der Energie 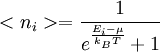
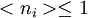 . Diese Bedingung ist mit der Fermi-Dirac-Statistik für jeden beliebigen Wert von
. Diese Bedingung ist mit der Fermi-Dirac-Statistik für jeden beliebigen Wert von 

