Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Pauli-PrinzipDas Pauli-Prinzip (auch paulisches Ausschlussprinzip) ist ein wichtiges, experimentell entdecktes Prinzip der Quantenmechanik. Es ist nach seinem Entdecker Wolfgang Pauli benannt. Es besagt, dass die Wellenfunktion asymmetrisch unter Vertauschung von Fermionen ist. Daraus ergibt sich insbesondere, dass Elektronen (oder andere Fermionen), die den gleichen Raum belegen, nicht in allen Quantenzahlen übereinstimmen dürfen. Eine Folge davon ist, dass normale Materie nicht beliebig kondensierbar ist. Produkt-Highlight
Spezielle Form (Pauli-Verbot)In seiner zuerst beobachteten und einfachsten Form gilt, dass in einem Atom keine zwei Elektronen in allen vier Quantenzahlen, die zu seiner Zustandsbeschreibung im Atommodell notwendig sind, übereinstimmen dürfen. Die relevanten Quantenzahlen im Atom sind dabei die Schale des Elektrons (Hauptquantenzahl), Unterschale (Nebenquantenzahl), der Spin der Elektronen (Spinquantenzahl) und die magnetische Quantenzahl. Allgemeine Form (verallgemeinertes Pauli-Prinzip)FormulierungDie Gesamtwellenfunktion
Dabei sind
AbleitungSind zwei Teilchen ununterscheidbar, muss das Betragsquadrat der Wellenfunktion gegenüber der Vertauschung invariant sein:
Somit beschränkt sich die Wirkung des Permutationsoperators auf die Änderung des komplexen Anteils der Wellenfunktion und der Vertauschung der Teilchen:
Weitere Anwendung des Permutationsoperators macht die Vertauschung rückgängig:
Um das Betragsquadrat konstant zu halten muss also gelten:
Somit kann man zwischen zwei Sorten Teilchen unterscheiden, solchen bei denen sich unter Permutation das Vorzeichen der Wellenfunktion ändert (Fermionen), und solchen, bei denen sich das Vorzeichen der Wellenfunktion unter Permutation nicht ändert (Bosonen). Anschauliche DeutungDie totale Antisymmetrie einer Wellenfunktion bedeutet, dass sie bei Vertauschung zweier beliebiger Teilchen ihr Vorzeichen wechselt. Physikalisch bedeutet die Antisymmetrie, dass zwei Fermionen niemals den selben Quantenzustand besetzen können: Stimmen nämlich zwei Fermionen in Ort und Spinquantenzahl überein, so verändert eine formale Vertauschung der beiden Fermionen aufgrund deren Ununterscheidbarkeit die Wellenfunktion nicht. Die einzige Lösung ist dann eine verschwindende Gesamtwellenfunktion wegen Ψ = − Ψ, also Ψ = 0. Bei einer Separation in Ortswellenfunktion und Spinwellenfunktion fordert die Antisymmetrie der Gesamtwellenfunktion bei symmetrischer Ortswellenfunktion eine antisymmetrische Spinwellenfunktion, und umgekehrt. Eine (anti)symmetrische Spinwellenfunktion kennzeichnet eine paarweise (anti)parallele Spinorientierung. Die triviale Lösung einer antisymmetrischen Ortswellenfunktion erhält man, wenn sich die paarweise vertauschten Teilchen am selben Ort befinden ( GültigkeitDas Pauli-Prinzip gilt für alle Fermionen (Teilchen mit halbzahligem Spin). Diese genügen der Fermi-Dirac-Statistik aufgrund des sogenannten Spin-Statistik-Theorems. Neben Fermionen gibt es auch Teilchen mit ganzzahligem Spin. Für diese so genannten Bosonen gilt das Pauli-Prinzip nicht. Sie genügen der Bose-Einstein-Statistik und können gleiche Quantenzustände besetzen (im Extremfall bis zum Bose-Einstein-Kondensat). Kurz zusammengefasst: Die Gesamtwellenfunktion ψ muss für Fermionen antisymmetrisch sein. Die Gesamtwellenfunktion ψ muss für Bosonen symmetrisch sein. KonsequenzenDas Pauli-Prinzip führt zur Austauschwechselwirkung und ist für die Spinordnung in Atomen (Hundsche Regeln) und Festkörpern (Magnetismus) verantwortlich. In der Astronomie wird durch das Pauli-Prinzip erklärt, dass alte Sterne, wie zum Beispiel weiße Zwerge oder Neutronensterne, nicht unter ihrer eigenen Gravitation zusammenbrechen. Hierbei erzeugen die Fermionen einen Gegendruck, der einer weiteren Kontraktion entgegenwirkt. Siehe auchUnunterscheidbare Teilchen, Kooperatives Phänomen, Ferromagnetismus, Antiferromagnetismus, Spindichtewelle |
|
| Dieser Artikel basiert auf dem Artikel Pauli-Prinzip aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





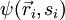 eines Systems von
eines Systems von 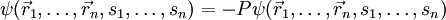 .
.
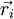 der Ort und
der Ort und 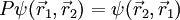 .
.
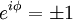 .
.
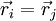 ).
).


