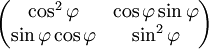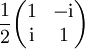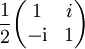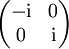Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Jones-VektorDer Jones-Vektor ist ein zweidimensionaler komplexwertiger Vektor, der zur Repräsentation der Polarisation ebener elektromagnetischer Wellen dient. Benannt wurde der Jones-Vektor nach R. Clark Jones, der dieses Verfahren zur Polarisationsdarstellung 1941 einführte. Der Jones-Formalismus eignet sich insbesondere zur Analyse optischer Systeme, in denen ein Lichtstrahl eine Kaskade von optischen Bauelementen durchläuft.
Produkt-HighlightIn komplexer Schreibweise hat die Elongation einer monochromatischen ebenen Welle in einem kartesischen Koordinatensystem die Orts- und Zeitabhängigkeit
wobei k die Wellenzahl und ω die Kreisfrequenz bezeichnen und als Ausbreitungsrichtung die z-Achse gewählt ist. Der Jones-Vektor dieser Welle ist dann einfach
d. h. die explizite Raum- und Zeitabhängigkeit der Amplitude wird bei der Beschreibung der Welle unterdrückt. Der Effekt eines optischen Bauelements auf den Jones-Vektor eines transmittierten Lichtstrahls lässt sich (sofern es keine nichtlinearen Eigenschaften hat) durch eine komplexwertige 2×2-Matrix A beschreiben,
Durchläuft der Lichtstrahl ein System optischer Elemente mit Jones-Matrizen A1...An, so lässt sich der Gesamteffekt des optischen Systems durch eine Jones-Matrix beschreiben (sofern Mehrfachreflexionen zwischen den einzelnen Komponenten keine Rolle spielen). Die Eigenpolarisationen eines optischen Systems entsprechen den Eigenvektoren seiner Jones-Matrix. Der Jones-Vektor eignet sich nur für die Beschreibung vollständig polarisierten Lichts, und entsprechend können nur optische Komponenten, die keine depolarisierenden Eigenschaften besitzen, durch Jones-Matrizen charakterisiert werden. Sind Depolarisationseffekte von Bedeutung, muss auf den aufwändigeren Stokes-Formalismus zurückgegriffen werden.
Gemäß der üblichen Sprechweise in der Optik, bezeichnen "H" wie horizontal und "V" wie vertikal die Orientierung in die x- und y-Richtung Literatur
|
||||||||||||||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Jones-Vektor aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


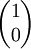
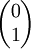
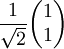
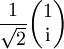
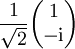



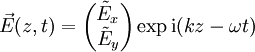 ,
,
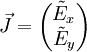 ,
,
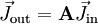 .
.
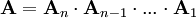
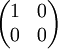
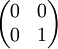
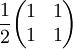
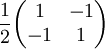
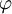 rad aus der V-Stellung gedreht
rad aus der V-Stellung gedreht