Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
K·p-MethodeVorlage:DISPLAYTITLE:k·p-Methode Die k·p-Methode (auch KP-Methode) ist eine Methode der Quantenphysik zur näherungsweisen Lösung der Schrödinger-Gleichung für Elektronen in Halbleitern und anderen Festkörpern und damit insbesondere zur Bestimmung der Bandstruktur des Festkörpers. Die Bezeichnung stammt daher, dass in den Energien der einzelnen Energiebänder ein Ausdruck der Form k·p, also das Skalarprodukt des Wellenvektors und des quantenmechanischen Impulsoperators auftritt. Produkt-HighlightDie k·p-Methode baut auf einer Beschreibung der Elektronen als nicht miteinander wechselwirkende Teilchen in einem effektiven periodischen Potential (das die Wechselwirkung mit den anderen Elektronen und die Atomkernen beschreibt) auf. Sie erlaubt es, aus den für einen Wellenvektor k0 des Elektrons bekannten Lösungen der Schrödinger-Gleichung die Lösungen für andere k-Werte und damit die Bandstruktur des Festkörpers zu bestimmen. Die Lösungen bei k=k0 müssen mit einer anderen Methode berechnet werden, oft geschieht das mit Hilfe der Dichtefunktionaltheorie, die beispielsweise für große Elementarzellen nur für k0=0, den sogenannten Γ-Punkt durchgeführt werden. Die Elektronenenergien für andere k-Werte werden dann daraus störungstheoretisch bestimmt. Mathematisch betrachtet, werden die Elektronenzustände als Blochwellen angeschrieben,
wobei die verschiedenen Elektronenzustände für einen k-Wert, also die Energiebänder, mit n nummeriert sind. Die Funktionen
Wenn wie hier N Bänder berücksichtigt werden, spricht man auch von der N-Band k ·p-Methode. Je größer N desto genauer ist die erhaltene Näherung. Die k·p-Methode wird vor allem in Rechnungen für Halbleitermaterialien verwendet; damit kann beispielsweise die effektive Masse der Elektronen und die Wechselwirkung mit Licht mit weniger Aufwand als bei einer vollständigen Rechnung bestimmt werden. Wichtig ist sie insbesondere im Fall entarteter Bänder, da der k·p-Term die Bänder miteinander koppelt und die Entartung teilweise aufhebt und neue Auswahlregeln für optische Übergänge zwischen den Bändern bestimmt. Mit den so erhaltenen Daten kann auch das elektronische Verhalten von Bauteilen der Mikroelektronik simuliert werden. Literatur
Kategorien: Quantenphysik | Festkörperphysik | Physikalische Chemie | Computerchemie | Quantenchemie |
| Dieser Artikel basiert auf dem Artikel K·p-Methode aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





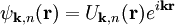 ,
,
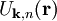 können nun als Linearkombinationen der Funktionen beim Referenzwert k0 dargestellt werden:
können nun als Linearkombinationen der Funktionen beim Referenzwert k0 dargestellt werden:
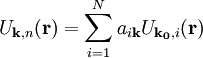 .
.


