Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
London-GleichungDie London-Gleichungen (nach Fritz und Heinz London) gehen von einem Postulat aus und ersetzen das ohmsche Gesetz in einem Supraleiter. Sie beschreibt damit auch, wie sich das Magnetfeld in einem solchen Stoff verhält. Ein Ergebnis ist etwa, dass das Magnetfeld trotz anderslautender Vorhersagen etwas in den Supraleiter eindringt (Eindringtiefe λL).
Produkt-Highlight
Experimentelle MotivationAufgrund des Meißner-Effektes ist ein Supraleiter ein idealer Diamagnet (magnetische Suszeptibilität χ=-1) und sein Inneres sollte magnetfeldfrei sein. Diese Vorhersage lässt sich aber experimentell nicht bestätigen. Es wird beobachtet, dass das Magnetfeld aus dünnen Supraleiterfilmen nicht ganz herausgedrängt wird, der Innenraum also nicht ganz feldfrei ist. Außerdem erhält sie die Stetigkeitsbedingung für das Magnetfeld am Rand des Supraleiters. London GleichungUm dies zu erklären ersetzt man das klassische Ohmsche Gesetz für die Stromdichte j und das elektrische Feld E: durch die London-Gleichung: wobei Es gibt noch zwei weitere nützliche Umformungen dieser Gleichung, die gelegentlich als 1. und 2. London Gleichungen bezeichnet werden: Die Phase S gibt keinen Beitrag zu diesen beiden Gleichungen. Zur ersten Gleichung nicht, weil die Phase nur ortsabhängig und somit zeitlich konstant ist. Zur zweiten Gleichung nicht, weil Achtung: Obwohl der Phasenanteil keinen Beitrag zu den letzten beiden Formeln liefert, darf er dennoch nicht vernachlässigt werden! Würde der Phasenanteil nicht eingehen, so würde das bedeuten, dass die Stromdichte ohne Magnetfeld Null sein müsste. In der Realität kann der Phasengradient jedoch auch noch einen Beitrag zur Stromdichte leisten, der dann nicht zwangsweise Null sein muss, d. h. die Stromdichte ist nicht Null, obwohl kein Magnetfeld anliegt. Der Ansatz einer makroskopischen Wellenfunktion wird auch für Supraflüssigkeiten gemacht. In diesem Fall ist es tatsächlich die Phase S, die etwa zum Fontäneneffekt oder zu quantisierten Vortexen führt. Theoretische Erklärung des Meißner-Effektes
Mit Hilfe der Maxwell-Gleichung Die Lösung dieser Gleichung beschreibt ein exponentielles Abklingen des Magnetfeldes innerhalb des Supraleiters, wie es im Experiment beobachtet wird (siehe Meißner-Effekt). Für ein homogenes Magnetfeld der Stärke B0 in z-Richtung, das an der Oberfläche des Supraleiter (senkrecht zur x-Achse) anliegt, lautet die Lösung: Das Magnetfeld klingt also im Supraleiter exponentiell ab, und zwar mit der Eindringtiefe λL, für die gilt: Dabei ist m die Ladungsträgermasse (hier die der Cooper-Paare), q die Ladung und n die Anzahldichte der supraleitenden Ladungsträger. Man erhält die Abschirmstromdichte: In einer dünnen Außenschicht des Supraleiters fließt also ein Abschirmstrom, senkrecht zum Magnetfeld. Makroskopische WellenfunktionAnsatz: Der supraleitende Zustand ist ein quantenmechanischer Zustand, der sich über makroskopische Längenskalen erstreckt. Er kann daher durch eine makroskopische Wellenfunktion beschrieben werden: Dabei wird davon ausgegangen, dass ψ eine konstante, reelle(!) Amplitude ψ0 hat und nur die Phase S ortsabhängig ist. Für den Impulsoperator in Anwesenheit eines Magnetfeldes gilt: Angewandt auf die Wellenfunktion ψ ergibt sich: Also: Mit Dies ist die oben angegebene London-Gleichung. Literatur
|
|||||||||||||
| Dieser Artikel basiert auf dem Artikel London-Gleichung aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |




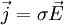
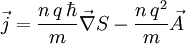
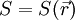 die Phase der makroskopischen Wellenfunktion ist (siehe letzter Abschnitt),
die Phase der makroskopischen Wellenfunktion ist (siehe letzter Abschnitt), 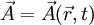 das
das 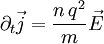
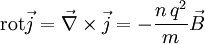
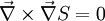 gilt.
gilt.
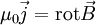 lässt sich die zweite London-Gleichung umschreiben:
lässt sich die zweite London-Gleichung umschreiben:
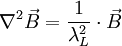
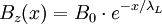
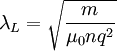
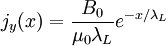
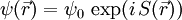
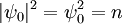 entspricht dabei der Teilchenzahldichte der
entspricht dabei der Teilchenzahldichte der 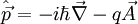
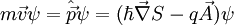
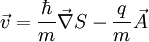
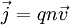 folgt unmittelbar:
folgt unmittelbar:


