Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
MagnetophononProdukt-Highlight
Magnetophonon-EffektDer Magnetophonon-Effekt (MPE) wurde 1961 von Gurevic und Firsov theoretisch vorhergesagt und 1963/64 in nInSb bei Untersuchungen der longitudinalen und transversalen magnetischen Widerstandsänderungen bei magnetischer Induktion B zwischen 1 und 3,5 T und Temperaturen um 77 K gefunden. In der Folgezeit ist dieser Effekt in einer größeren Anzahl von Halbleitermaterialien nachgewiesen und zur Untersuchung der Energiebandstruktur, des Phononensprektrums und der Elektron-Phonon-Wechselwirkung herangezogen worden.
SachverhaltDer MPE stellt einen besonderen Typ von im Magnetfeld auftretenden oszillatorischen galvanomagnetischen und thermomagnetischen Effekten, annähernd periodisch 1/B dar. Er unterscheidet sich vom ebenfalls in B − 1 periodischen Shubnikov-deHaas-Effekt dadurch, daß die Lage der Extrema fast unabhängig von der Ladungsträgerkonzentration beobachtet wird. Er hat seine Ursache in der Wechselwirkung zwischen Ladungsträgern in das durch das Magnetfeld gequantelten Energiezuständen (Landau-Niveaus) und Gitterschwingungen bei dominierender inelastischer Streuung an optischen Phononen. Es wird zwischen dem transversalen MPE, der in senkrecht zum Magnetfeld beobachteten Transporteigenschaften in Erscheinung tritt und dem longitudinalen MPE, der in Transporteffekten parallel zum Magnetfeld auftritt unterschieden. Der transversale MPE beruht auf der resonanten Streuung eines Elektrons zwischen zwei Landau-Niveaus durch Wechselwirkung mit optischen Phononen, die Resonanzgleichung lautet:
Dabei gibt
den Zusammenhang zwischen Energie EN,S und Wellenzahlvektor kz in Richtung des Magnetfeldes B für jedes Landau-Niveau N=0, 1, 2, ... und die beiden möglichen Spinzustände
erfüllt, letztere, wenn infolge genügend starker Spin-Bahn-Wechselwirkung Spin-Übergänge auftreten (Spin-MPE). Die den longitudinalen MPE hervorrufenden Streuprozesse sind nicht resonant, ändern aber immer dann, wenn die Bedingung
erfüllt ist, plötzlich ihre Intensität. Diese so genannten Pseudoresonanzen sind infolge der Beteiligung elastischer Streuung häufig verwaschen. Kennwerte, FunktionenDer MPE ist bei der Messung des Magnetowiderstandes, des Seebeck-Effekts im Magnetfeld, des Nernst-Ettinghausen-Effekts, der Photoleitung und des photoelektromagnetischen Effekts, im akustoelktrischen Effekt, im Hall-Effekt und bei der Raman-Streuung beobachtet worden. Für das Beobachten des MPE gibt es eine vom Material abhängige optimale Temperatur Topt, die durch die Phononenenergie und die Trägerbeweglichkeit bestimmt wird. Das maximale Magentfeld Bmax, überhalb welchem Einphononen-Resonanzübergänge verwschwinden, hängt über ωc = ω0 von der Phononenenergie und der effektiven Masse meff ab. Die untere Magnetfeldgrenze wird durch die thermische bzw. Stoßverbreiterung der Landau-Niveaus gegeben. AnwendungenDer MPE wird zur Untersuchung von Materialeigenschaften von Halbleitern herangezogen. Der Effekt ist in den Transportgrößen nicht sehr stark ausgeprägt. Zur genaueren Erfassung sind differentielle Messtechniken erforderlich. Untersuchungen zur Energiebandstruktur. Gemäß den Gleichungen (1) bzw. (5) und (2) ist es möglich, die Landau-Aufspaltung von Valenz- und Leitungsband und daraus effektiven Massen und den Zusammenhang zwischen Energie und Quasiimpuls im Energiebereich bis zu mehreren Bestimmung der Elektron-Phonon-Kopplung. Umgekehrt gibt die Auswertung des MPE in Halbleitern mit bekannter Bandstruktur die Möglichkeit, die Energie der an der Streuung beteiligten optischen Phononen und eventuell auch der akustischen Phononen mit geringer Dispersion vom Rand der Brillouin-Zone zu bestimmen. Die relativen Streuwahrscheinlichkeiten von verschiedenen inelastischen Elektron-Phonon-Wechselwirkungen, die gleichzeitig auftreten, beispielsweise Intra- und Intervalley-Streuprozesse, können aus einem Vergleich der Höhen der entsprechenden Resonanzsignale ermittelt werden. Mehrphononenübergänge lassen sich nachweisen, und die Wahrscheinlichkeit für Spin-Umklapp-Streuprozesse kann abgeschätzt werden. Bestimmung von Deformationspotentialen. Aus der Verschiebung der Resonanzlagen unter hydrostatischem Druck kann unter der meist erfüllten Voraussetzung, daß die Phononenenergie nur wenig beeinflusst wird, der Druckkoeffizient der effektiven Masse berechnet werden. Bei Untersuchungen unter uniaxialem Druck lassen sich außerdem Energieparameter der Elektron-Phonon-Wechselwirkung, insbesondere die Deformationspotentiale, bestimmen. Untersuchung der Trägeraufheizung bei optischer und elektrischer Anregung. Die Amplituden der MP-Serien widerspiegeln die Elektronenbesetzung höherer Landau-Niveaus. Aus dem Vergleich der Fourier-Komponenten der MP-Oszillationen ist die Berechnung der Energieverteilung, insbesondere der Eletronentemperatur, möglich. Aus aus Untersuchung der Resonanzbreiten lssaen sich Elektronentemperaturen angeregter Ladungsträgerverteilungen bestimmen. Bei elektrischer Anregung wird meistens der longitudinale MPE untersucht, bei optischer Anregung, wo das Magnetfeld keinen Einfluss auf den Anregungsmechanismus hat, der transversale. Quellen
Kategorien: Quantenphysik | Festkörperphysik | Magnetismus |
|
| Dieser Artikel basiert auf dem Artikel Magnetophonon aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





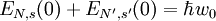 . (1)
. (1)
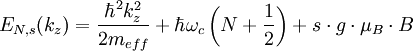 (2)
(2)
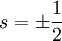 an,
an, 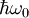 ist die Energie der optischen Phononen,
ist die Energie der optischen Phononen, 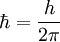 , h –
, h – 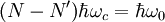 bei s = s' bzw. (3)
bei s = s' bzw. (3)
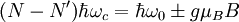 (4)
(4)
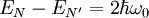 (5)
(5)


