Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Landau-NiveauDie Landau-Niveaus (nach Lew Dawidowitsch Landau) stellen eine Quantelung der Energie von geladenen Teilchen dar, die sich in homogenen Magnetfeldern bewegen. Man kann diese Aufspaltung zum Beispiel mit dem De-Haas-van-Alphen-Effekt nachmessen. Man kann zeigen (Herleitung siehe unten), dass die Energie eines geladenen Teilchens der Masse μ (z. B. eines Elektrons), das parallel zu einem Magnetfeld B fliegt lautet: Dabei ist vz die (beliebige) Geschwindigkeit in z-Richtung und Die Landau-Niveaus lassen sich vor Allem in der Festkörper-Physik messen (De-Haas-van-Alphen-Effekt). Dort sind auch die transversalen Impulse aufgrund des Kristallgitters gequantelt. Es lässt sich dann zeigen, dass auf jedem Landau-Zylinder exakt gleichviele Zustände liegen.
Produkt-Highlight
Theoretische HerleitungVoraussetzungen und AufgabenstellungMan betrachte eine einfache Situation: Ein Teilchen der Masse μ und der Ladung q befindet sich in einem homogenen Magnetfeld Man kann leicht zeigen, dass sich daraus über Man erhält dann die (zunächst noch klassische) Hamilton-Funktion dieses Systems zu: Indem man die Orts- und Impulsvariablen durch die entsprechenden quantenmechanischen Operatoren ersetzt, erhält man daraus den Hamiltonoperator des Systems. Im letzten Teil der obigen Gleichung wurde ein „Geschwindigkeitsoperator“ definiert, der folgende Form hat: Aus der klassischen Behandlung weiß man, dass die Lösung des Problems eine Helixbewegung in z-Richtung ist. Darum ist es sinnvoll (was sich in den späteren Rechnungen auch zeigen wird), die folgende Aufteilung des Hamilton-Operators vorzunehmen: Man erhält für den „Geschwindigkeitsoperator“ Dabei wurde die Zyklotronfrequenz Damit vertauschen auch Eigenwerte von H||Es gilt folgende Vertauschungsrelation: Damit ist ein Satz über Operatoren, die nach obiger Relation vertauschen, anwendbar und wir können schließen, dass Damit beschreibt also Eigenwerte von H⊥Um die Energieeigenwerte von Damit hat dann Die Energieeigenwerte von Eine genauere Betrachtung zeigt, dass diese Eigenwerte unendlichfach entartet sind. Darauf deutet bereits die Tatsache hin, dass Eigenwerte von HDie Gesamtenergie ergibt sich aus der Summe der Eigenenergien von Diese Niveaus bezeichnet man als Landau-Niveaus. Sie sind unendlichfach entartet (siehe oben). Je nach angelegtem Magnetfeld erhält man damit für ein festes vz unterschiedliche Niveauabstände. Es gilt: Literatur
Kategorien: Festkörperphysik | Quantenphysik |
|
| Dieser Artikel basiert auf dem Artikel Landau-Niveau aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


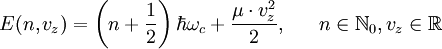
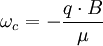 die Zyklotronfrequenz. Dies bedeutet, dass (wie rechts in der Abbildung angedeutet) nur bestimmte Teilchenbahnen erlaubt sind, die durch die zwei Quantenzahlen vz und n charakterisiert werden. Man kann sich die Bewegung auch so vorstellen, dass sich das Teilchen longitudinal frei ausbreitet und transversal (radial) dazu eine harmonische Schwingungsbewegung ausführt (siehe
die Zyklotronfrequenz. Dies bedeutet, dass (wie rechts in der Abbildung angedeutet) nur bestimmte Teilchenbahnen erlaubt sind, die durch die zwei Quantenzahlen vz und n charakterisiert werden. Man kann sich die Bewegung auch so vorstellen, dass sich das Teilchen longitudinal frei ausbreitet und transversal (radial) dazu eine harmonische Schwingungsbewegung ausführt (siehe 


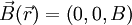 , das nur eine Komponente in z-Richtung aufweist. Dieses Feld kann auch durch folgendes
, das nur eine Komponente in z-Richtung aufweist. Dieses Feld kann auch durch folgendes 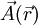 dargestellt werden:
dargestellt werden:
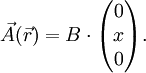
 wieder obiges Magnetfeld ergibt.
wieder obiges Magnetfeld ergibt.
![H(\vec{r},\vec{p})=\frac{1}{2\mu}\left[\vec{p}-q\cdot\vec{A}(\vec{r})\right]^2= \frac{1}{2\mu}\left[p_x^2+(p_y - qBx)^2+p_z^2\right]=\frac{1}{2}\mu\vec{V}^2](images/math/c/0/a/c0aabc2d9d98aed481202337dadc36f5.png)
![\vec{V}=\frac{1}{\mu}\left[\vec{p}-q\cdot\vec{A}(\vec{r})\right]=\frac{1}{\mu}\begin{pmatrix}p_x\\p_y-q\cdot B\cdot x\\p_z\end{pmatrix}](images/math/a/1/3/a139855417e28cbe1b9ba3a09b934893.png)
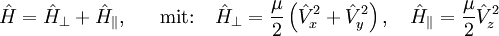
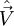 folgende Vertauschungsrelation:
folgende Vertauschungsrelation:
![\left[\hat{V}_x, \hat{V}_y\right]=\frac{1}{\mu^2}\left(\left[\hat{P}_x, \hat{P}_y\right]-qB\cdot\left[\hat{P}_x, \hat{X}\right]\right)=i\hbar\frac{qB}{\mu^2}=-i\cdot\frac{\hbar\omega_c}{\mu}.](images/math/9/6/2/96216ef0efa89b2e686ce2dcca8febe9.png)
![\left[\hat{V}_x, \hat{V}_z\right]=\left[\hat{V}_y, \hat{V}_z\right]=0](images/math/4/6/1/46147998bc75b5c39bad6f073be7f79c.png)
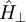 und
und 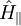 miteinander und es gibt eine Basis von gemeinsamen Eigenvektoren zu
miteinander und es gibt eine Basis von gemeinsamen Eigenvektoren zu ![\mu\cdot\left[\hat{Z}, \hat{V}_z\right]=\left[\hat{Z}, \hat{P}_z\right]=i\hbar.](images/math/2/e/3/2e33bebe0675c82829392c8a1c7bbd43.png)
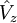 ein kontinuierliches Spektrum von Eigenwerten vz hat. Weiterhin sind alle Eigenvektoren von
ein kontinuierliches Spektrum von Eigenwerten vz hat. Weiterhin sind alle Eigenvektoren von 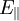 von
von 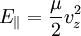
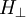 (und damit die sog. Landau-Niveaus) zu erhalten, führt man folgende Operatoren mit ihrer Vertauschungsrelation ein:
(und damit die sog. Landau-Niveaus) zu erhalten, führt man folgende Operatoren mit ihrer Vertauschungsrelation ein:
![\hat{Q}=\sqrt{\frac{\mu}{\hbar\omega_c}}\cdot \hat{V}_y,\ \ \ \ \ \ \hat{S}=\sqrt{\frac{\mu}{\hbar\omega_c}}\cdot \hat{V}_x,\ \ \ \ \ \left[\hat{Q}, \hat{S}\right]=\frac{\mu}{\hbar\omega_c}\cdot\left[\hat{V}_y, \hat{V}_x\right]=i](images/math/9/a/2/9a2dba3bf1b1ec5d66da3331ff271ce2.png)