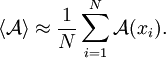Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Monte-Carlo-SimulationMonte-Carlo-Simulation oder Monte-Carlo-Studie, auch: MC-Simulation ist ein Verfahren aus der Stochastik, bei dem sehr häufig durchgeführte Zufallsexperimente die Basis darstellen. Es wird aufgrund der Ergebnisse versucht, mit Hilfe der Wahrscheinlichkeitstheorie analytisch unlösbare Probleme im mathematischem Kontext numerisch zu lösen. Als Rechtfertigung wird dabei vor allem das Gesetz der großen Zahl gesehen. Die Zufallsexperimente können entweder real durchgeführt werden, etwa durch Würfeln, oder durch die Erzeugung von Zufallszahlen. Heutzutage können computergenerierte Zufallsvorgänge in beinahe beliebig großem Umfang simuliert werden. Produkt-Highlight
ÜberblickFür die Anwendung der Monte-Carlo-Simulation kommen vor allem folgende Problemgruppen in Betracht:
Der Name leitet sich vom monegassischen Stadtteil Monte Carlo ab, der durch seine Spielbank berühmt wurde. Mathematisch betrachtetMathematisch ist das System ein wahrscheinlichkeitsgewichteter Weg im Phasenraum (allg. Zustandsraum). Monte-Carlo-Simulationen sind besonders geeignet, um statistische Mittelwerte einer Größe
oder hochdimensionale Integrale (Monte-Carlo-Integration) wie
zu berechnen. P(x) soll in diesem Zusammenhang ein normiertes statistisches Gewicht (z.B. ein Boltzmanngewicht) sein. Häufig ist der Raum Ω so groß, dass die Summation nicht vollständig durchgeführt werden kann. Stattdessen erzeugen wir nun eine Markow-Kette
Dieser Zusammenhang basiert auf dem Gesetz der großen Zahlen. Je nach physikalischem System kann es schwierig sein, diese Markow-Kette zu erzeugen. Insbesondere muss man sicherstellen, dass die Markow-Kette tatsächlich den gesamten Raum Ω bedeckt und nicht nur einen Teil des Raumes abtastet. Man sagt, der Algorithmus muss ergodisch sein. Anwendungen und spezielle MethodenPythia (Lund)Simulations-Programm für die Teilchenphysik. Dabei werden möglichst viele verschiedene Äste eines Zerfall-Baumes realisiert, indem man bei jeder Astgabel per pseudorandom einen Ast realisiert. SHERPASimulations-Programm für die Hochenergie-Teilchenphysik. Entstanden an der TU Dresden, wird es inzwischen von einer international verteilten Arbeitsgruppe um Dr. F. Krauss entwickelt. Metropolis Monte CarloDie von Metropolis et al. publizierte Methode zur Untersuchung statistisch-mechanischer Systeme mittels Computersimulation leitet sich von der Monte-Carlo-Integration ab. Sequentielle Monte-Carlo-Methoden (SMC)Sequentielle Monte Carlo (SMC) Methoden eignen sich zur Bayesschen Zustandsschätzung von dynamischen Systemen. Ziel der SMC-Methoden ist es, den Systemzustand als Funktion der Zeit auf Basis von einer Reihe Beobachtungen des Systems und A-priori-Kenntnissen der Systemdynamik zu schätzen. Dazu wird die komplizierte Wahrscheinlichkeitsdichte des Zustandes diskret durch eine Menge von Partikeln approximiert. Sequentielle Monte-Carlo Methoden werden auch Partikelfilter genannt. Quanten-Monte-Carlo-MethodenQuanten-Monte-Carlo-Methoden werden zur Berechnung von physikalischen Observablen in quantenfeldtheoretischen Modellen benutzt. Beispiele sind Modelle aus der theoretischen Festkörperphysik wie das Hubbard-Modell oder das tJ-Modell. Quellen
Siehe auch
Links
|
|
| Dieser Artikel basiert auf dem Artikel Monte-Carlo-Simulation aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





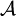 ,
,
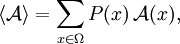
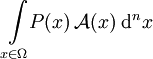
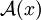 ist der Wert der Größe
ist der Wert der Größe 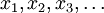 von Zuständen in
von Zuständen in