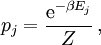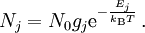Boltzmann-Statistik

Die Boltzmann-Statistik (auch: Gibbs-Boltzmann-Verteilung, nach Josiah Willard Gibbs und Ludwig Boltzmann) gibt die Wahrscheinlichkeit eines Zustandes eines Systems an, welches im thermodynamischen Gleichgewicht an ein Wärmebad der Temperatur T gekoppelt ist, also ein Repräsentant eines kanonischen Ensembles ist.

Weiteres empfehlenswertes Fachwissen

Dauerhaft genaue Prüfgewichte dank 12 kostenloser Tipps

Tägliche Sichtkontrolle der Laborwaagen

Wie kann man Pipetten schnell überprüfen?

Wir nehmen dabei an, dass die Zustände durchnummeriert sind mit j = 1,2,...N, mit der jeweils zugehörigen Energie E_j. Die Wahrscheinlichkeit, dass man den Zustand j misst, ist

wobei die Normierung Z auch Zustandssumme genannt wird. Man erhält die Boltzmann-Statistik aus der Annahme der a priori gleich wahrscheinlichen Zustände im abgeschlossenen Gesamtsystem, welches das Wärmebad und das betrachtete (Unter-)System, das sich im thermischen Gleichgewicht mit dem Wärmebad befindet, enthält. Die dabei unbestimmt bleibende Konstante β erhält man durch Anschluss an die Thermodynamik: β = 1 / k_BT, mit der Boltzmann-Konstante k_B.

Anstelle von Wahrscheinlichkeiten lässt sich die Boltzmann-Statistik auch durch Teilchenzahlen ausdrücken:

Hierbei bezeichnet N_j die Zahl der Teilchen, die den Zustand j besetzen, N₀ die Teilchenzahl des 0-ten Zustands und g_j den Entartungsgrad des Zustands j (also die Anzahl von Zuständen gleicher Energie E_j).

Die Boltzmann-Statistik ist anwendbar für alle möglichen klassischen und quantenmechanischen Systeme: magnetische Eigenschaften in Festkörpern, Phononen, Gase usw. Sie definiert u. a. die Empfindlichkeit spektroskopischer Methoden (vgl. NMR).

Für klassische Systeme wie z. B. ideale Gase wird die Darstellung schwieriger, da die Energien der Zustände kontinuierlich dicht liegen und damit aus der Wahrscheinlichkeit eine Wahrscheinlichkeitsdichte wird. Dabei muss das richtige Maß gefunden werden, was Gibbs heuristisch mit 1 / h³ pro Teilchen angegeben hat, was allerdings erst durch die später entstandene Quantentheorie sinnvoll interpretiert werden konnte: das hier eingeführte h wurde das Plancksche Wirkungsquantum.

Der zu den Zuständen gehörige 6N-dimensionale Phasenraum ist durch die Menge aller kontinuierlichen Orte und Impulse aller Gasteilchen gegeben. Das heißt wenn die Zustandssumme über ein Phasenraumintegral berechnet wird, muss entsprechend die Vielfachheit des Zustandes berücksichtigt werden, was in einem Gas mit N ununterscheidbaren Teilchen einfach 1 / N! ist. Dies nennt man auch die korrigierte Boltzmannabzählung.