Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Rarita-Schwinger-GleichungIn der theoretischen Physik ist die Rarita-Schwinger Gleichung eine relativistische Feldgleichung für Spin-3/2-Fermionen. Sie ist ähnlich aufgebaut wie die Dirac-Gleichung für Spin-1/2-Fermionen und kann aus dieser hergeleitet werden. Sie wurde erstmals 1941 von William Rarita und Julian Schwinger formuliert und veröffentlicht. In einer modernen Notation wird sie folgendermaßen angeschrieben: Produkt-HighlightDabei ist εμνρσ das Levi-Civita-Symbol. γ5 und γν sind dabei die üblichen Dirac-Matrizen. m ist die Ruhemasse und ψμ ist ein vektorwertiger Spinor. μ = 0,1,2,3 ist ein Lorentz-Index und ψμ besteht damit aus insgesamt 16 komplexwertigen Funktionen. Dies entspricht der Die Feldgleichung kann formal aus der folgenden Lagrange-Dichte durch Variation der unabhängigen Felder Re(ψμ) und Im(ψμ) hergeleitet werden: Dabei bezeichnet berücksichtigt werden. Die Rarita-Schwinger-Gleichung hat für Teilchen mit Ruhemasse 0 eine Eichsymmetrie bezüglich der Eichtransformation Von der Rarita-Schwinger-Gleichung existieren auch Weyl- und Majorana-Darstellungen, die sich bezüglich der physikalischen Ergebnisse nicht von der Originalgleichung unterscheiden. Sie wird gewöhnlich dazu benutzt zusammengesetzte Teilchen, wie das Delta (Δ) Baryon zu beschreiben und zu untersuchen. Manchmal wird diese Gleichung auch für hypothetische Teilchenfelder wie das Gravitino verwendet. Zu beachten bleibt, dass bisher noch kein stabiles Elementarteilchen mit Spin 3/2 experimentell nachgewiesen werden konnte. Artikel
Bücher
|
| Dieser Artikel basiert auf dem Artikel Rarita-Schwinger-Gleichung aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





 Darstellung der Lorentz-Gruppe. Diese Darstellung ist isomorph zur Untergruppe
Darstellung der Lorentz-Gruppe. Diese Darstellung ist isomorph zur Untergruppe  .
.
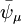 den adjungierten Spinor zu
den adjungierten Spinor zu 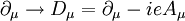
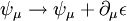 . Dabei ist
. Dabei ist 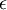 ein frei wählbares, komplexes Eichfeld.
ein frei wählbares, komplexes Eichfeld.


