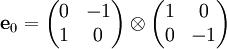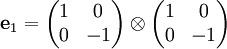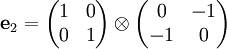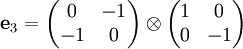Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
SpinorEin Spinor ist in der Mathematik, und dort speziell in der Differentialgeometrie, ein Vektor in einer kleinsten Darstellung (ρ,V) einer Spin-Gruppe. Die Spin-Gruppe ist isomorph zu einer Teilmenge einer Clifford-Algebra, jede Clifford-Algebra ist isomorph zu einer Teil-Algebra einer reellen, komplexen oder quaternionischen Matrix-Algebra. Diese hat eine kanonische Darstellung durch Spaltenvektoren, die Spinoren. Ein Spinor ist in der Physik meist ein Vektor einer 2-dimensionalen komplexen Darstellung der Spin-Gruppe Spin(1,3), die zur Gruppe der Lorentz-Transformationen SO(1,3) des Minkowski-Raums gehört. Produkt-Highlight
Spinoren der QuantenphysikStruktur der Gruppe Spin(1,3)Die Gruppe Spin(1,3) ist eine Teilmenge des geraden Teils Cℓ0(1,3) der Clifford-Algebra Cℓ(1,3). Die gesamte Algebra wird von den 4 kanonischen Basisvektoren e0,e1,e2,e3 des 4-dimensionalen Minkowski-Raums M4 mit quadratischer Form (in Koordinaten dieser Basis) Die Unteralgebra Cℓ0(1,3) der geraden Elemente wird erzeugt von zweifachen Produkten, die e0 enthalten, :f1:=e0e1, :f2:=e0e2, :f3:=e0e3. Diese antikommutieren ebenfalls, ihre Quadrate haben den Wert 1. Die fehlenden zweifachen Produkte bilden eine „doppelt gerade“ Unteralgebra, die von geraden Produkten der fk erzeugt wird:
Die von den gk erzeugte Unteralgebra ist isomorph zur Algebra der Quaternionen. Mit Rücksicht auf die Pauli-Matrizen identifizieren wir g1=j; g2=k; g3=i, genaueres weiter unten. Unter den Basisvektoren der geraden Unteralgebra fehlt noch das Volumenelement
Dieses kommutiert mit der gesamten geraden Unteralgebra, es gilt ω²=-1. Isomorphe MatrixalgebraEs ist leicht zu sehen, dass (ω,g1,g2) die gerade Unteralgebra erzeugen und dass der ungerade Teil der Algebra als Cℓ1(1,3)=e0Cℓ0(1,3) zu erhalten ist. Insgesamt gilt:
Dies liefert den Isomorphismus φ
der eingeschränkt einen Isomorphismus ergibt. Es sei im folgenden immer ℂ=ℝ[i], wobei i eine imaginäre Einheit der Quaternionen ist. Dann kann der Isomorphismus wie folgt definiert werden:
Als Folge daraus ergeben sich mit fk = ωgk und ek = -e0fk
Darstellung in den Quaternionen, Majorana-SpinorenEs gibt einen Isomorphismus Darstellung in den komplexen Zahlen, Weyl-SpinorenWir definieren eine bijektive Abbildung
d. h. einem Element φ(c)=w⊗q aus gegeben ist, zugeordnet. Dabei ist z. B.
Die Matrix dieser Abbildung ist die erste Pauli-Matrix σ1, analog gilt f2↦σ2 und f3↦σ3. Somit ist ρW eine komplex zweidimensionale Darstellung der geraden Unteralgebra und damit auch der Spin(1,3)-Gruppe. Diese Darstellung von Zu dieser gibt es eine konjugierte Darstellung Dirac-, Weyl- und Majorana-SpinorenEine treue Darstellung ist eine Einbettung der Algebra in eine Matrixgruppe, oder generell in die Endomorphismengruppe eines Vektorraums. Dabei sollen Elemente der Spin-Gruppe auf orthogonale oder unitäre Matrizen abgebildet werden. Dazu folgendes Lemma: Sind A, B selbstadjungierte unitäre Abbildungen auf V mit A²=B²=I und AB=-BA, so zerfällt V in isomorphe, zueinander orthogonale Unterräume V+:=ker(I-A) und V-:=ker(I+A)=BV+. Das Tripel (V,A,B) lässt sich isomorph abbilden auf
I+ ist die Identität auf 'V+. Das auftretende Tensorprodukt kann hier auch als das Kronecker-Produkt von Matrizen aufgefasst werden. Weyl-SpinorenEine Weyl-Spinor-Darstellung, nach Hermann Weyl, ist eine kleinste komplexe Darstellung von Spin(1,3). Diese ist gleichzeitig auch die kleinste komplexe Darstellung der geraden Unteralgebra Cℓ0(1,3). Angenommen, wir hätten eine komplexe Darstellung (ρ,V) von Cℓ0(1,3) in einen hermiteschen Vektorraum V vorliegen. Dabei sind die Bilder ρ(fk) (der Kürze wegen lassen wir im weiteren das ρ weg) unitäre, selbstadjungierte Abbildungen von V in sich.
übergehen. Um die Gestalt von f2 einzuschränken, betrachten wir das Produkt f1f2 und stellen fest, dass aufgrund der Vertauschungsregeln
sich folgende Gestalt zwingend ergibt
Da der Vektorraum V+ komplex ist, können wir ihn in zueinander orthogonale Unterräume V++ und V+- aufspalten, auf welchen g12 wie i oder -i wirkt. Beide Unterräume ergeben separate Darstellungen, die jeweils minimalen sind zueinander komplex konjugiert, die Matrizen sind die Pauli-Matrizen, denn wenn g12=i, so ist
Im minimalen Fall ist V++=ℂ, V+-={0} oder umgekehrt. Es gibt also zwei konjugierte Weyl-Spinor-Darstellungen. Dirac-SpinorenIn der Quantenelektrodynamik bzw. Atiyah-Singer-Indextheorie wird der Dirac-Operator definiert. Das „wie“ ist nicht wichtig, nur, dass eine Darstellung der gesamten Clifford-Algebra benötigt wird. Die Dirac-Spinor-Darstellung, nach Paul Dirac, ist die kleinste komplexe Darstellung von Cℓ(1,3). Ist eine solche komplexe Darstellung gegeben, so können wir wie oben die Darstellung der geraden Unteralgebra analysieren. Um auch den ungeraden Teil zu bestimmen, betrachten wir das Bild von e1. Es kommutiert mit f3 und antikommutiert mit f1, wie oben stellen wir fest, dass
Man überzeugt sich, dass g1 die Unterräume V++ und V+- vertauscht, wir können also die Darstellung durch eine noch weiter Faktorisierte ersetzen:
Die minimale Dirac-Spinor-Darstellung ist wieder die mit V++=ℂ (und jede dazu isomorphe). Majorana-SpinorenDie Majorana-Spinor-Darstellung, nach Ettore Majorana, sowohl der Spin-Gruppe als auch der Clifford-Algebra ist die kleinste reelle Darstellung von Cℓ(1,3). Wir können die Analyse von oben übernehmen bis zu der Stelle, an welcher g1 und g12 auf V+ definiert sind. Hier können wir nun V+ nach A=g1 zerlegen in V++:=ker(I-A) und V+-:=ker(I+A), B=g12 vertauscht beide Unterräume, allerdings ist B²=-I, somit
Nach Ausmultiplizieren erhalten wir für V++=ℝ
|
|
| Dieser Artikel basiert auf dem Artikel Spinor aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





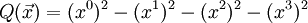 erzeugt. Dementsprechend antikommutieren die Produkte verschiedener Basisvektoren, für ihre Quadrate gilt v²=-Q(v), also (e0)² = -1, (e1)² = (e2)² = (e3)² = 1.
erzeugt. Dementsprechend antikommutieren die Produkte verschiedener Basisvektoren, für ihre Quadrate gilt v²=-Q(v), also (e0)² = -1, (e1)² = (e2)² = (e3)² = 1.
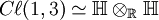 ,
,
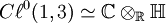
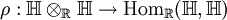 , der einem Tensorprodukt a⊗b die Abbildung
, der einem Tensorprodukt a⊗b die Abbildung 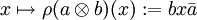 zuordnet. Damit ist
zuordnet. Damit ist 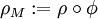 eine quaternionisch eindimensionale oder reell vierdimensionale Darstellung der gesamten Clifford-Algebra. Als letzteres hat sie den Namen Majorana-Spinor-Darstellung, nach Ettore Majorana.
eine quaternionisch eindimensionale oder reell vierdimensionale Darstellung der gesamten Clifford-Algebra. Als letzteres hat sie den Namen Majorana-Spinor-Darstellung, nach Ettore Majorana.
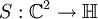 als
als 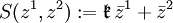 . Diese Abbildung ist reell linear und komplex rechts antilinear, d. h.
. Diese Abbildung ist reell linear und komplex rechts antilinear, d. h. 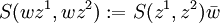 . Sei
. Sei 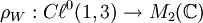 , durch
, durch 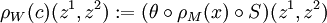 ,
,
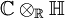 wird die Abbildung, die durch
wird die Abbildung, die durch
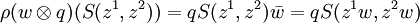
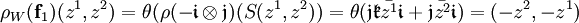 .
.
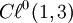 heißt Weyl-Spinor-Darstellung, nach Hermann Weyl.
heißt Weyl-Spinor-Darstellung, nach Hermann Weyl.
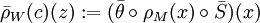 , wobei
, wobei 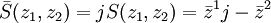
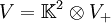 ,
, 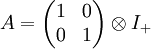 ,
, 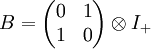
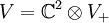 mit
mit 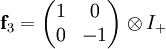 und
und 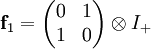
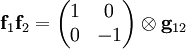 mit
mit 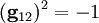 .
.
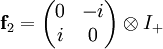 .
.
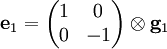 mit
mit 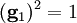 .
.
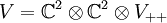 mit den Bildern der Generatoren
mit den Bildern der Generatoren


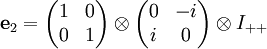
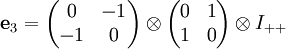
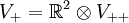 mit
mit 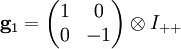 und
und 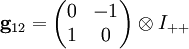
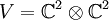 mit den Bildern der Generatoren
mit den Bildern der Generatoren