Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Stern-Gerlach-VersuchMit Hilfe des Stern-Gerlach-Versuchs wurde 1922 von den Physikern Otto Stern und Walther Gerlach erstmals die Richtungsquantelung von Drehimpulsen von Atomen beobachtet. Der Stern-Gerlach-Versuch ist ein grundlegendes Experiment in der Physik und wird immer wieder herangezogen, um die Natur der Quantenmechanik zu erläutern. Produkt-HighlightPrinzip des Stern-Gerlach-VersuchsAus einem Atomstrahlofen werden Silberatome ausgedampft, dieser Strahl wird mit Hilfe zweier Blenden kollimiert und durchläuft ein inhomogenes Magnetfeld. Auf einem Schirm schlägt sich das Silber nieder. Entgegen der klassisch erwarteten, kontinuierlichen Verteilung der Silberatome werden zwei voneinander getrennte "Silberflecken" detektiert (siehe Abbildung links), dies ist nur mit einer quantenmechanischen Deutung zu erklären. Erklärung
Die Gesamtheit der Bahndrehimpulse sowie der Spins der Elektronen eines Atoms erzeugt ein magnetisches Moment. Ist der Bahndrehimpuls und Spin der Gesamtheit aller Elektronen in einem Atom nicht gleichzeitig verschwindend, verkompliziert sich die Situation, da dann Gesamtdrehimpuls und das erzeugte magnetische Moment Bei Silber, welches von Stern und Gerlach verwendet wurde, ist es so, dass nur das 5s-Elektron zum Gesamtdrehimpuls beiträgt, da sich die Spins und Drehimpulse der restlichen Elektronen nach der Hundschen Regel aufheben. Dieses 5s Elektron hat die Bahndrehimpulsquantenzahl l=0 (es besitzt keinen Bahndrehimpuls) und somit trägt bei Silber nur der Spin des äußersten Elektrons zum Gesamtdrehimpuls bei. Das heißt, dass das magnetische Moment Videos
Kategorien: Magnetismus | Quantenmechanik | Atomphysik |
| Dieser Artikel basiert auf dem Artikel Stern-Gerlach-Versuch aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





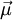 des Atoms nicht mehr die gleiche Richtung haben (siehe:
des Atoms nicht mehr die gleiche Richtung haben (siehe: 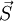 ist.
Bringt man nun ein solches Atom in ein Magnetfeld wie es von Stern und Gerlach erzeugt wurde und sich in der Form
ist.
Bringt man nun ein solches Atom in ein Magnetfeld wie es von Stern und Gerlach erzeugt wurde und sich in der Form 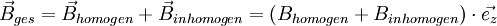 darstellen lässt, wird eine Quantisierungsachse (hier die z-Achse) vorgegeben, wonach der Spin in z-Richtung nur die Einstellmöglichkeiten
darstellen lässt, wird eine Quantisierungsachse (hier die z-Achse) vorgegeben, wonach der Spin in z-Richtung nur die Einstellmöglichkeiten 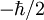 oder
oder 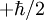 hat (auch "Spin Down" und "Spin Up" genannt). Hierbei soll darauf hingewiesen werden, dass ein klassischer Drehimpuls sich in beliebiger Richtung zu dieser Achse einstellen kann.
Durch das inhomogene Feld wirkt nun eine Kraft
hat (auch "Spin Down" und "Spin Up" genannt). Hierbei soll darauf hingewiesen werden, dass ein klassischer Drehimpuls sich in beliebiger Richtung zu dieser Achse einstellen kann.
Durch das inhomogene Feld wirkt nun eine Kraft  auf das magnetische Moment des Atoms, da
auf das magnetische Moment des Atoms, da 

