Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Landé-FaktorDer Landé-Faktor (nach Alfred Landé) beschreibt den Zusammenhang zwischen dem
Drehimpuls und dem magnetischem Moment
eines Elementarteilchens, Atomkerns oder Atoms. Der Drehimpuls wird dabei in
Einheiten von Produkt-Highlight
VeranschaulichungWir stellen uns ein klassisches Elektron vor, das sich auf einer Kreisbahn bewegt. Nach den Gesetzen der Elektrodynamik erzeugt dieser Kreisstrom ein magnetisches Dipolfeld. Dieses Dipolfeld wird durch das magnetische Moment beschrieben. Über das Dipolfeld (bzw. das magn. Moment) wechselwirkt das kreisende Elektron mit einem äußeren magnetischen Feld. Zum anderen besitzt das kreisende Elektron auch einen (Bahn-)Drehimpuls bezüglich des Zentrums der Kreisbewegung. Man kann nun innerhalb der klassischen Physik zeigen, dass der Zusammenhang zwischen dem magnetischen Moment und dem Drehimpuls des kreisenden Elektrons durch gegeben ist, d.h. der Landé-Faktor der Bahnbewegung des Elektrons ist exakt 1. Landé-Faktor des ElektronsIn der Quantenmechanik wird gezeigt, dass Elektronen eine klassisch nicht erklärbare Eigenschaft, den Spin, besitzen. Dieser verhält sich wie ein Drehimpuls und hängt mit dem magnetischen Moment zusammen. Der Zusammenhang ist ähnlich, er lautet wobei Bestimmung des Landé-Faktors des ElektronsDie Bestimmung des Landé-Faktors des Elektrons hat eine interessante Geschichte. Das Experiment gibt einen Wert von etwa 2. Die theoretische Beschreibung des Elektrons durch die (nichtrelativistische) Schrödinger-Gleichung kennt zunächst keinen Elektronspin. Man muss ihn künstlich einbauen. Genauso steht es mit dem magnetischen Moment des Elektrons aufgrund seines Spins. Das Ergebnis ist die (nichtrelativistische) Pauli-Gleichung. Die relativistisch quantenmechanische Beschreibung des Elektrons durch die Dirac-Gleichung für Spin-½-Fermionen bringt dann eine überraschende Erkenntnis: Sowohl der Spin als auch ein Landé-Faktor von exakt 2 wird von der Dirac-Gleichung sozusagen automatisch vorausgesagt. Genauere Experimente zeigten dann geringe Abweichungen des Landé-Faktors von 2. Die Theorie musste also noch weiter verfeinert werden, da das elektromagnetische Feld nicht in seiner quantisierten Form in die Dirac-Gleichung eingeht. Die Quantisierung des elektromagnetischen Feldes führt zur Quantenelektrodynamik. Die Aussage dieser Theorie zum Wert des Landé-Faktors ist etwas diffiziler als in den vorausgegangenen Fällen: Die Antwort lässt sich mathematisch nicht exakt berechnen. Vielmehr muss eine Störungsrechnung angewandt werden, was zulässig ist, da die Abweichungen von g vom Wert 2 klein sind und somit als Störungen aufgefasst werden können. Man rechnet zunächst eine Näherung aus. Dann eine Korrektur zur Näherung. Dann eine weitere Korrektur und so fort. Der exakte Wert kann so immer besser angenähert werden. (Die Näherungen sind im vorliegenden Fall die Vertexkorrekturen eines Elektron-Photon-Vertex; sie können durch Feynman-Diagramme dargestellt werden.) Die Näherungen liefern für den Landé-Faktor des Elektrons einen theoretischen Wert von wohingegen das genaueste Experiment einen Wert von für den Landé-Faktor des Elektrons ergibt. Dies ist wohl die genaueste Übereinstimmung von Experiment und Theorie, die eine Naturwissenschaft je erbracht hat. Bestimmung des Landé-Faktors eines AtomsFür ein Atom errechnet sich der dem Gesamtdrehimpuls S ist dabei die Summe der Elektronenspins, L ist die Summe der Bahndrehimpuls-Quantenzahlen und J=L+S bei mehr als halb-vollen Schalen und sonst J=L-S. Für die Berechnung werden nur die Valenzelektronen hergenommen, die sich nach den Hundschen Regeln auf die verschiedenen Niveaus der höchst besetzten Schale verteilen, da die Drehimpuls- und Spin-Quantenzahlen abgeschlossener Schalen zu Null koppeln. Siehe auchKategorien: Atomphysik | Quantenphysik |
|
| Dieser Artikel basiert auf dem Artikel Landé-Faktor aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


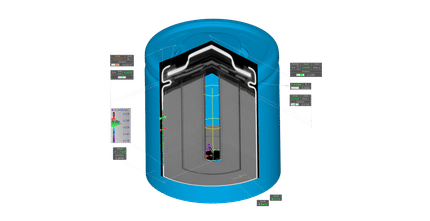
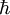 und das magnetische Moment in Einheiten des
und das magnetische Moment in Einheiten des


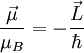
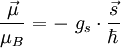
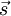 der Spin und
der Spin und 
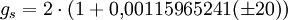
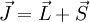 zugehörige Landé-Faktor näherungsweise (dh. ohne Korrekturen der
zugehörige Landé-Faktor näherungsweise (dh. ohne Korrekturen der