Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Zweite QuantisierungDie Zweite Quantisierung ist ein quantenmechanischer Formalismus zur Behandlung von Vielteilchenproblemen. Im wesentlichen handelt es sich dabei um eine Umformulierung der „normalen“ Quantenmechanik in eine Form, welche die fundamentalen Symmetrierelationen bosonischer und fermionischer Wellenfunktionen implizit enthält (Symmetrisierungen und Antisymmetrisierungen sind in Ausdrücken der Zweiten Quantisierung also automatisch vorhanden und müssen nicht erst von Hand hinzugefügt werden). Die Bezeichnung „zweite Quantisierung“ kommt daher, dass in diesem Fall nicht nur die Zustände des Teilchens quantisiert sind, sondern auch die Felder (z.B. das elektrische Feld). Bei einer Einführung in die Quantenmechanik sind für gewöhnlich nur die Zustände des Teilchens quantisiert und die Felder werden als klassisch angesehen. Diesen einfacheren Fall nennt man gelegentlich „erste Quantisierung“. Des Weiteren erlaubt die Einführung des Fock-Raumes (s.u.) über die Umformulierung hinaus aber auch einen neuen physikalischen Aspekt: In der zweiten Quantisierung sind reine quantenmechanische Zustände ohne fest definierte Teilchenzahl möglich. Die Zweite Quantisierung wird im Bereich der Festkörperphysik, der Quantenfeldtheorien und anderen Vielteilchentheorien angewandt. Sie ist häufig der angemessenste Rahmen, um physikalische Probleme zu behandeln. Produkt-Highlight
Mathematische KonstruktionSei
Man kann also jede Vielteilchen-Wellenfunktion als Linearkombination solcher Determinanten-Zustände darstellen (bzw. entsprechender Permanenten-Zustände im bosonischen Fall). Diese Determinantenzustände sind neben der rein mathematischen Bedeutung als Entwicklungsbasis häufig auch von großer physikalischer Bedeutung, da sich Grundzustands-Wellenfunktionen nichtwechselwirkender Systeme als reine Determinantenzustände (bzw. Permanentenzustände) darstellen lassen. Was man nun also tut, ist diesen Determinantenzuständen neue Namen zuzuordnen: Der Determinante/Permanente zur Konfiguration
zu, mit n1 = Anzahl Vorkommen des Wertes von l1 in L, n2 = Anzahl Vorkommen des Wertes von l2 in L, .... Die Werte nj nennt man Besetzungszahlen der zugehörigen Basiszustände. Die Besetzungszahlen können bei Fermionen nur 1 oder 0 sein, da sonst die Determinante verschwinden würde (zwei gleiche Spalten). In dieser Bezeichnungsweise ist also die allgemeine Darstellung eines N-Teilchen Vielteilchenzustands
die Besetzungszahldarstellung. Der antisymmetrische bzw. symmetrische N-Teilchen-Hilbertraum HN wird also durch diese Zustände
Da sich Operatoren unabhängig von der konkreten Teilchenzahl darstellen lassen (s. u.), ist diese Konstruktion sinnvoll. In diesem Raum sind Zustände unbestimmter Teilchenzahl enthalten (Linearkombination von Zuständen verschiedener bestimmter Teilchenzahlen). In ihm wird Vielteilchentheorie normalerweise betrieben. Einzelne Determinantenzustände, die, wie schon gesagt z. B. besondere Zustände eines wechselwirkungsfreien Systems sein könnten, kann man in der Form Erzeugungs-, Vernichtungs- und TeilchenzahloperatorenMan führt nun, zunächst recht willkürlich, neue Operatoren ein, die Teilchen im Basiszustand (Definition auf der Basis des Zustandsraumes, auf den Rest durch lineare Fortsetzung). Im bosonischen Fall:
Im fermionischen Fall:
Die Vorfaktoren sorgen dabei jeweils für das Nichtauftreten unmöglicher Zustände (z. B. mit Besetzungszahlen < 0 oder > 1 bei Fermionen), für das Wegkapseln der Antisymmetrie bei Fermionen in anderen Ausdrücken und dafür, dass sich die Besetzungszahloperatoren in beiden Fällen als
ergeben. Nachrechnen (oder scharfes Hingucken) zeigt, dass diese Operatoren bei Determinantenzuständen die Besetzungszahlen reproduzieren:
VertauschungsrelationenFür die so konstruierten Operatoren gelten im fermionischen Fall die Antivertauschungsrelationen
wobei [A,B] + : = AB + BA den Antikommutator bedeutet. Im bosonischen Fall gelten die Vertauschungsrelationen
[A,B]: = AB − BA ist der Kommutator. Ein- und ZweiteilchenoperatorenEs lässt sich zeigen, dass sich sämtliche linearen Operatoren auf dem Fockraum als Linearkombination von Polynomen in den Erzeugungs/Vernichtungsoperatoren darstellen lassen. Darin liegt ein wesentlicher Aspekt ihrer Wichtigkeit. Besonders bedeutend sind dabei die sogenannten Einteilchen- bzw. Zweiteilchen-Operatoren, die ihrem Namen nach entweder Observablen einzelner Teilchen repräsentieren (z.B. kinetische Energie, Position, Spin) oder Wechselwirkungen zwischen zwei Teilchen (z. B. Coulomb-Wechselwirkung zwischen zwei Elektronen). Es ergeben sich dabei einfache Ausdrücke: Sei
ein Einteilchen-Operator (d. h. jedes hα wirkt nur auf die Koordinaten des
wobei
Bei den Ausdrücken handelt es sich um echte Gleichheit der Operatoren, so lange sie auf eine feste Teilchenzahl bezogen sind. Man sieht aber, dass die zweitquantisierte Form der Operatoren die Teilchenzahl nicht mehr explizit enthält. Die zweitquantisierten Operatoren nehmen in Systemen verschiedener Teilchenzahl also jeweils die selbe Form an. Konkrete BeispieleEinteilchen-Op.Teilchendichte in Zweitquantisierung bezüglich Impulsbasis (diskrete Impulsbasis, endliches Volumen mit periodischen Randbedingungen):
Coulomb-WechselwirkungIn Zweitquantisierung bezüglich (diskreter) Impulsbasis.
Transformation zwischen EinteilchenbasenErzeugungs- und Vernichtungsoperatoren bezüglich einer gegebenen Einteilchenbasis
Durch diese Beziehungen ist es möglich, einen Basiswechsel im Fockraum durchzuführen und somit gegebene Ausdrücke auf für die gerade anliegende Situation besser geeignete Formen zu transformieren. Auf ähnliche Art werden aus den Erzeugungs/Vernichtungs Operatoren für diskrete Einteilchenbasen auch Feldoperatoren bezüglich kontinuierlicher Orts- bzw. Impulsbasen erzeugt, wie sie vor allem in den Quantenfeldtheorien verwendet werden. |
|
| Dieser Artikel basiert auf dem Artikel Zweite_Quantisierung aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





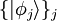 eine orthonormale Einteilchen-Basis eines quantenmechanischen Systems (d.h. ein Satz an Wellenfunktionen, nach denen sich jede beliebige Einteilchenwellenfunktion entwickeln lässt). Dann ist bekannt, dass sich jede fermionische (bosonische) Vielteilchen-Wellenfunktion, die ja von Natur aus antisymmetrisch (symmetrisch) ist, nach Determinanten (Permanenten) bezüglich dieser Einteilchenbasis entwickeln lässt:
Sei
eine orthonormale Einteilchen-Basis eines quantenmechanischen Systems (d.h. ein Satz an Wellenfunktionen, nach denen sich jede beliebige Einteilchenwellenfunktion entwickeln lässt). Dann ist bekannt, dass sich jede fermionische (bosonische) Vielteilchen-Wellenfunktion, die ja von Natur aus antisymmetrisch (symmetrisch) ist, nach Determinanten (Permanenten) bezüglich dieser Einteilchenbasis entwickeln lässt:
Sei 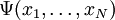 antisymmetrisch (
antisymmetrisch (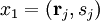 , z. B. Orts- und Spinkoordinaten z.B. eines Elektrons). Dann gibt es komplexe Zahlen
, z. B. Orts- und Spinkoordinaten z.B. eines Elektrons). Dann gibt es komplexe Zahlen 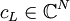 (d.h. zu jeder „Konfiguration“
(d.h. zu jeder „Konfiguration“ 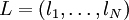 (
(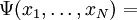
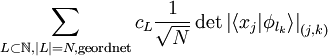
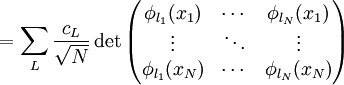
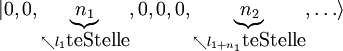
 :
:
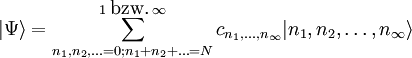
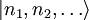 mit
mit 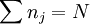 aufgespannt. Es liegt nun nahe, einen allgemeineren Raum, den Fock-Raum einzuführen, der durch die
aufgespannt. Es liegt nun nahe, einen allgemeineren Raum, den Fock-Raum einzuführen, der durch die 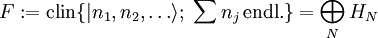 .
.
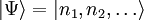 eindeutig angeben, wenn man dazu sagt, auf welche Einteilchenbasis man sich bezieht.
Siehe auch:
eindeutig angeben, wenn man dazu sagt, auf welche Einteilchenbasis man sich bezieht.
Siehe auch: 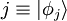 „erzeugen“ bzw. „vernichten“ (d. h. die entsprechende Besetzungszahl erhöhen oder verringern):
„erzeugen“ bzw. „vernichten“ (d. h. die entsprechende Besetzungszahl erhöhen oder verringern):
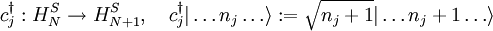
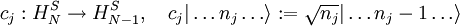
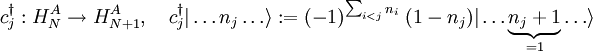
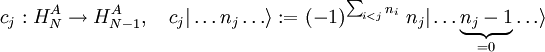
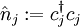
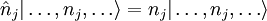 .
.
![[c_i, c_j^\dagger]_+ = \delta_{ij} \qquad [c_i, c_j]_+ = 0 \qquad [c_i^\dagger, c_j^\dagger]_+ = 0,](images/math/1/1/a/11a40e47088568b21e05450911cc12b9.png)
![[c_i, c_j^\dagger] = \delta_{ij} \qquad [c_i, c_j] = 0 \qquad [c_i^\dagger, c_j^\dagger] = 0.](images/math/2/b/7/2b75eab81791ed3e48432036787afd37.png)
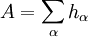
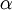 -ten Teilchens, von der Struktur her sind die
-ten Teilchens, von der Struktur her sind die 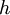 s aber alle gleich) so ergibt sich (durch ausrechnen):
s aber alle gleich) so ergibt sich (durch ausrechnen):
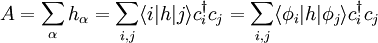
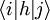 das Matrixelement des Einteilchenoperators ist, aus dem sich die
das Matrixelement des Einteilchenoperators ist, aus dem sich die 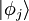 , bezüglich denen quantisiert wurde.
Für Zweiteilchenoperatoren ergibt sich analog:
, bezüglich denen quantisiert wurde.
Für Zweiteilchenoperatoren ergibt sich analog:
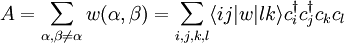
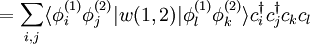 .
.
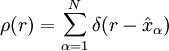
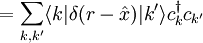
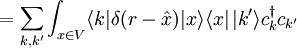
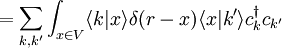
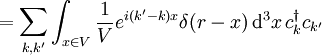
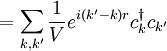
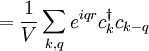
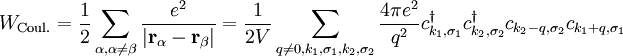
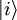 lassen sich durch
entsprechende Operatoren bezüglich einer anderen Einteilchenbasis
lassen sich durch
entsprechende Operatoren bezüglich einer anderen Einteilchenbasis 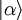 ausdrücken:
ausdrücken: