Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Aharonov-Bohm-EffektDer Aharonov-Bohm-Effekt (nach David Bohm und Yakir Aharonov) ist ein quantenmechanisches Phänomen, bei dem ein Magnetfeld In der Quantenmechanik beschreibt man das Verhalten eines geladenen Teilchens im Magnetfeld durch den Hamilton-Operator (q: Ladung des Teilchens, Klassisch dagegen erfolgt die Beeinflussung durch die sog. Lorentzkraft des Magnetfeldes, nach der Bewegungsgleichung wobei Vektorpotential Das Vektorpotential Weiteres empfehlenswertes Fachwissen
ExperimentIm Experiment laufen geladene Teilchen (Elektronen) auf verschiedenen Seiten an einem Zylinder vorbei, in dem ein Magnetfeld B herrscht. Der Zylinder ist von einer Wand umgeben, die von den Teilchen nicht durchdrungen werden kann; außerhalb ist das Magnetfeld Null. Trotzdem hängt der Ausgang des Experiments davon ab, ob das Magnetfeld ein- oder ausgeschaltet ist, denn das Vektorpotential A ist im ersten Fall auch außerhalb des Zylinders vorhanden. (Man stelle sich hierbei ein radial verlaufendes Vektorpotential vor. Dessen Rotation rot A und damit das Magnetfeld B ist außerhalb des Zylinders Null, dennoch ist A nirgends Null.) Die Superposition der Wellenfunktionen hinter dem Zylinder ergibt ein Interferenzmuster, das vom Vektorpotential beeinflusst wird, da die Wellenfunktionen auf Wegen rechts und links des Zylinders eine unterschiedliche Phasenverschiebung erhalten. Experimentell wurde dieser Zusammenhang u.a. von Möllenstedt et al. gezeigt. InterpretationManchmal wird aus dem Effekt der Schluss gezogen, dass das Vektorpotential in der Quantenmechanik eine fundamentalere Bedeutung habe als das zugehörige Kraftfeld. Das trifft nicht das Wesentliche: Letztlich ist der magnetische Fluss ΦB entscheidend. Dieser kann durch ein Kurvenintegral ausgedrückt werden, wobei der Integrationsweg sich außerhalb des Bereiches mit Man kann den Effekt auch so interpretieren, dass durch den Magnetfluss die Geometrie verändert wird (nichtkommutative Geometrie). Die geschlossene Kurve Γ entspricht dabei der Burgers-Schleife in der Theorie der Versetzungen und das Magnetfeld Literatur
Siehe auch
|
|
| Dieser Artikel basiert auf dem Artikel Aharonov-Bohm-Effekt aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


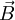 die
die 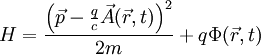
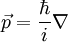 :
: 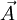 : Vektorpotential,
: Vektorpotential, 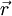 : Ort und m: Masse des Teilchens)
: Ort und m: Masse des Teilchens)
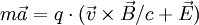
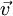 bzw.
bzw. 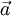 Geschwindigkeit bzw. Beschleunigung des Teilchens sind und
Geschwindigkeit bzw. Beschleunigung des Teilchens sind und 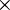 das Vektorprodukt bedeutet. Klassisch ist also ein Effekt nur dort zu erwarten, wo das Magnetfeld
das Vektorprodukt bedeutet. Klassisch ist also ein Effekt nur dort zu erwarten, wo das Magnetfeld 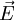 , das hier unwesentlich ist, ebenso wie das elektrische Potential
, das hier unwesentlich ist, ebenso wie das elektrische Potential 
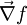 einer beliebigen skalaren Funktion
einer beliebigen skalaren Funktion 


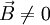 befinden darf. Es gilt jedenfalls
befinden darf. Es gilt jedenfalls 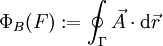 , wobei
, wobei 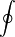 angedeutet wird, damit man es mit einer eichinvarianten, d. h. nicht von der oben erwähnten Funktion f abhängigen Größe zu tun hat. Die Fläche F hängt über
angedeutet wird, damit man es mit einer eichinvarianten, d. h. nicht von der oben erwähnten Funktion f abhängigen Größe zu tun hat. Die Fläche F hängt über 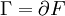 mit der geschlossenen Kurve
mit der geschlossenen Kurve 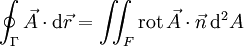 , ist dieses Linienintegral über die geschlossene Kurve
, ist dieses Linienintegral über die geschlossene Kurve 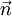 ist der Normalenvektor auf der Fläche und
ist der Normalenvektor auf der Fläche und 

