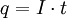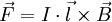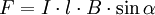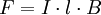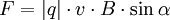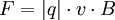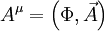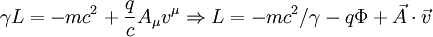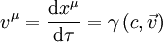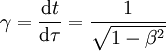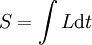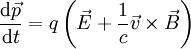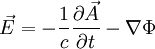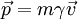Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
LorentzkraftDie Lorentzkraft ist nach Hendrik Antoon Lorentz die Kraft, die auf bewegte elektrische Ladungen in elektromagnetischen Feldern wirkt. Im allgemeinen Sprachgebrauch wird oft nur die magnetische Komponente als Lorentzkraft bezeichnet.
Produkt-Highlight
Lorentzkraft auf einen stromdurchflossenen LeiterEin elektrischer Strom in einem Leiter besteht aus bewegten elektrischen Ladungen. Befindet sich der Leiter in einem Magnetfeld, wird daher eine Kraft auf ihn ausgeübt. Wie oben zu sehen ist, ist die Lorentzkraft proportional zur Geschwindigkeit Kraft auf eine bewegte Ladung q: Ist Eingesetzt ergibt sich: Die Stromstärke ergibt sich aus der Anzahl von Ladungsträgern q, die sich pro Zeiteinheit t durch einen Querschnitt des Leiters bewegen:
Eingesetzt ergibt sich damit: Wenn man die Länge von Die entsprechende Betragsgleichung lautet: wobei α der Winkel zwischen Leiter und Magnetfeld ist. Die Richtung der Kraft geht aus dieser Gleichung nicht hervor und muss separat hergeleitet werden, vgl. oben, Lorentzkraft auf eine bewegte Ladung. Im speziellen Fall eines Leiters, der senkrecht zum Magnetfeld verläuft, ist sinα = 1. Damit lässt sich der Betrag der Lorentzkraft besonders einfach berechnen: Lorentzkraft auf eine bewegte LadungDie vom Magnetfeld verursachte Lorentzkraft ist sowohl zu den magnetischen Feldlinien als auch zur Bewegungsrichtung der Ladung senkrecht und lenkt die betroffene Ladung ab, ohne den Betrag ihrer Geschwindigkeit zu verändern. (Beweis folgt über die Ableitung des Betrages nach der Zeit, die das Skalarprodukt aus Beschleunigung und Geschwindigkeit enthält. Dieses verschwindet, da die Kraft (bzw. die Beschleunigung) senkrecht zur Bewegungsrichtung (bzw. der Geschwindigkeit) ist.) Im allgemeinen Fall berechnet sich der Vektor der magnetischen Komponente der Lorentzkraft mit folgendem Kreuzprodukt: Wobei Die entsprechende Betragsgleichung (mit α als Winkel zwischen Wenn sich ein geladenes Teilchen senkrecht zum Magnetfeld bewegt ist sinα = 1. Damit lässt sich der Betrag der Lorentzkraft besonders einfach berechnen: Während sich bei der Vektorrechnung die Richtung der Kraft automatisch richtig ergibt, muss sie bei der Betragsrechnung separat hergeleitet werden. Dabei hilft die Drei-Finger-Regel oder die Rechte-Faust-Regel. Diese Regeln berücksichtigen – korrekt angewandt – sowohl die Polarität der Ladung als auch deren Bewegungsrichtung im Magnetfeld. Theorie der LorentzkraftDie Lorentzkraft kann als Axiom aufgefasst oder aus der Lagrangeschen Formulierung der Elektrodynamik hergeleitet werden. Das elektromagnetische Feld ist durch das Viererpotential gegeben. Für die Lagrangefunktion eines geladenen Teilchens mit Ladung q und Masse m gilt Hierbei ist die Vierergeschwindigkeit gegeben durch die Ableitung der Koordinaten xμ nach der Eigenzeit τ: mit dem Zusammenhang zwischen Eigenzeit und Zeit im Inertialsystem des Beobachters
mit β = v / c. Das Prinzip von Hamilton verlangt die Stationarität der Wirkung und das führt auf die Euler-Lagrange-Gleichungen Einsetzen unserer Lagrangefunktion für ein geladenes Teilchen im EM-Feld liefert die Bewegungsgleichung Hierbei sind die Felder durch definiert und der Impuls lautet
BeispieleWenn man im stillstehenden Auto bei laufendem Motor das Licht (oder die Heckscheibenheizung oder beides) einschaltet, sinkt ganz kurz die Drehzahl ab, bis die Motorsteuerung die Drehzahl wieder stabilisiert hat. Das passiert, weil sich die Lichtmaschine plötzlich „schwerer“ drehen lässt. Jede Kraft erfordert eine Gegenkraft. Immer wenn Energie „verbraucht“ wird (in der Glühlampe) muss sie ja irgendwo herkommen. Energielieferant im Auto ist der Kraftstoff. Der Strom, den ein Generator abgibt, kann durch den so genannten Erregerstrom, der über Spulen ein Magnetfeld im Generator erzeugt, gesteuert werden. Ist kein Magnetfeld vorhanden, gibt der Generator keinen Strom ab und benötigt auch keine Antriebsleistung, sondern läuft im Leerlauf. Dort wird nur sehr wenig Leistung zur Überwindung der Reibung benötigt. Technisch angewandt wird die Lorentzkraft
Auch die Ablenkung des Sonnenwinds durch die Magnetfelder der Erde und anderer Planeten ist auf die Lorentzkraft zurückzuführen. Siehe auch
|
|
| Dieser Artikel basiert auf dem Artikel Lorentzkraft aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


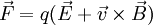
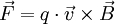
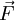 Kraft
Kraft
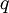 Elektrische Ladung
Elektrische Ladung
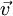 Geschwindigkeit der Ladung
Geschwindigkeit der Ladung
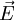
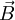
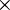 Vektorprodukt
Vektorprodukt



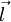 der Weg, den die Ladung
der Weg, den die Ladung 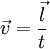
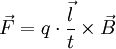
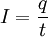 , wenn
, wenn