Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
VektorpotentialIn der klassischen Elektrodynamik, einem Teilgebiet der Physik, wird das Vektorpotential Produkt-HighlightDefinitionDas Vektorpotential gilt. Hierbei ist In der Elektrodynamik gilt die obige Formel unverändert, wohingegen für das elektrische Feld gilt. Hierbei ist Φ das skalare Potential. Diese beiden Ansätze, zusammen mit der Lorenz-Eichung, werden benutzt, um die Maxwellgleichungen zu entkoppeln. In der Magnetostatik wird für gewöhnlich die Coulomb-Eichung benutzt, die den statischen Grenzfall der Lorenzeichung darstellt. Eigenschaften des Vektorpotentials(1) Das Vektorpotential ist nur bis auf ein Gradientenfeld bestimmt, denn für jede skalare Funktion
(2) Das Vektorpotential ist als Vektorfeld nicht konservativ. Andernfalls wäre es durch den Gradienten eines skalaren Feldes α darstellbar und es würde gelten: (3) In der Magnetostatik kann das Vektorpotential über die Coulomb-Eichung quellfrei gemacht werden, das bedeutet
(4) In der Elektrodynamik, d.h. bei nicht-statischen Verhältnissen, benutzt man dagegen meist die sog. Lorenz-Eichung, nämlich folgende Beziehung, die für die Berechnung elektromagnetischer Wellenfelder nützlich ist:
(5) In der Magnetostatik erfüllt das Vektorpotential die Poisson-Gleichung, für die gilt
Die Ausdrücke (6) In der Elektrodynamik erweitert sich die Poisson-Gleichung zur (inhomogenen) Wellengleichung für das Vektorpotential
Die Lösung dieser Gleichung ist das sog. retardierte Vektorpotential
(7) Die drei Komponenten Ax, Ay und Az des Vektorpotentials und das skalare Potential Φ / c können in der Elektrodynamik zu einem sog. Vierervektor zusammengefasst werden, der sich bei den sog. Lorentz-Transformationen der Speziellen Relativitätstheorie Albert Einsteins wie das Quadrupel (x, y, z ,ct) transformiert. c ist dabei die Vakuum-Lichtgeschwindigkeit. |
| Dieser Artikel basiert auf dem Artikel Vektorpotential aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


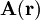 als mathematisches Hilfsmittel verwendet, um den Umgang mit der
als mathematisches Hilfsmittel verwendet, um den Umgang mit der 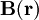 (anschaulich: das "Magnetfeld") zu vereinfachen. Es lässt sich verwenden, um die
(anschaulich: das "Magnetfeld") zu vereinfachen. Es lässt sich verwenden, um die 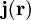 hervorgeht. Man kann also das Vektorpotential zu einer gegebenen Stromverteilung berechnen und daraus dann die magnetische Induktion
hervorgeht. Man kann also das Vektorpotential zu einer gegebenen Stromverteilung berechnen und daraus dann die magnetische Induktion 


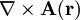 die Rotation des Vektorpotentials. Durch diesen Ansatz ist automatisch die Divergenz von
die Rotation des Vektorpotentials. Durch diesen Ansatz ist automatisch die Divergenz von 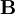 Null.
Null.
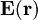
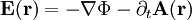
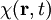 gilt
gilt
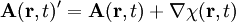
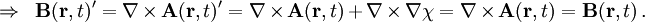
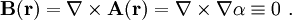
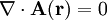 .
.
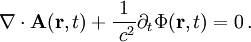 Dabei ist
Dabei ist 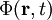 das sog. skalare Potential (s.u.).
das sog. skalare Potential (s.u.).
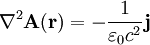 .
.
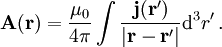
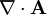 und
und 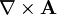 werden von anderen Autoren auch als
werden von anderen Autoren auch als 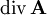 bzw.
bzw. 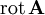 bezeichnet.
bezeichnet.
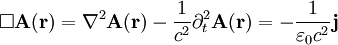 ,
,
 der
der 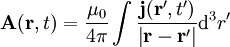 , mit
, mit 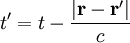 .
.


