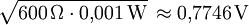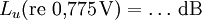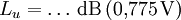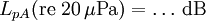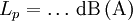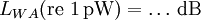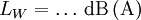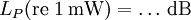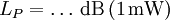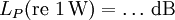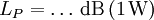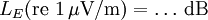Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Bel (Einheit)
Das Bel (B) ist eine nach Alexander Graham Bell benannte Hilfsmaßeinheit zur Kennzeichnung von Pegeln und Maßen. Diese logarithmischen Größen finden ihre Anwendung unter anderem in der Akustik (z. B.: Schalldruckpegel, Schalldämm-Maß), der Hochfrequenztechnik als Teil der Nachrichtentechnik (z. B.: SNR), der Tontechnik und der Automatisierungstechnik. In der Praxis ist die Verwendung des zehnten Teils eines Bels (Dezibel, Einheitenzeichen dB) üblich. Produkt-Highlight
Definition, Bel und Dezibel
Das Bel dient zur Kennzeichnung des dekadischen Logarithmus des Verhältnisses zweier gleichartiger Leistungs- bzw. Energiegrößen P1 und P2:
Ein Bel (B) ist der Wert von L, wenn P1 / P2 = 10. Das gebräuchlichere Dezibel (dB) wird mit Hilfe des Einheitenvorsatzes „Dezi“ (Symbol „d“) gebildet:
Das Quadrat der Effektivwerte von Feldgrößen x (z. B. elektrische Spannung, Schalldruck), die auf ein lineares System einwirken, ist proportional zu den entsprechenden Leistungs- bzw. Energiegrößen P, d. h.
Soll von Feldgrößen ausgehend ein Pegel oder Maß berechnet werden, muss das Verhältnis der Quadrate dieser Größen verwendet werden und es gilt
Zu beachten ist dabei, dass die Größen x1 und x2 stets die gleiche Einheit haben müssen. Ein Beispiel für eine so definierte Größe ist der Schalldruckpegel. Umrechnung in die Einheit NeperDezibel und Neper stehen in einem festen linearen Verhältnis zueinander:
Durch Umstellen nach dB und Umrechnung der Logarithmenbasis folgt daraus:
Dezibel und Neper, Historische EntwicklungObwohl nicht das Bel bzw. Dezibel, sondern das Neper die zum Internationalen Einheitensystem SI kohärente Hilfsmaßeinheit[1] für logarithmische Verhältnisgrößen ist, wird in der Praxis überwiegend das Dezibel verwendet. Das hat zum einen historische Gründe:[2] In den USA war bis 1923 als Einheit für das Dämpfungsmaß einer Fernsprechverbindung die Hilfsmaßeinheit „Mile Standard Cable“ (m.s.c.) in Verwendung. Diese Einheit entspricht dem Dämpfungsmaß eines bestimmten Kabeltyps („19 gauge“) bei einer Länge von einer englischen Meile und einer Frequenz von 800 Hz und gleichzeitig der mittleren subjektiven Wahrnehmbarkeitsschwelle beim Vergleich von zwei Lautstärken. Letzteres trifft ebenfalls für das Dezibel zu. Deshalb ergaben sich bei Verwendung des Dezibels in etwa die gleichen Zahlenwerte wie bei Verwendung von „Mile Standard Cable“ (1 m.s.c. = 0,9221 dB). Ein weiterer Grund für die bevorzugte Verwendung des Dezibels ist, dass sich einfacher fassbare Zahlenwerte ergeben, so entspricht z. B. die Verdopplung der Leistung einer Änderung um ca. 3 dB, die Verzehnfachung einer Änderung um 10 dB. Verwendung mit anderen Maßeinheiten, AnhängselSo wie jede andere Maßeinheit kann das Bel bzw. Dezibel zusammen mit anderen Maßeinheiten verwendet werden, wenn damit eine Größe beschrieben wird, bei der ein Pegel oder Maß durch Multiplikation oder Division mit einer anderen Größe verknüpft wird. Beispiele dafür sind das Dämpfungsmaß einer Leitung in Dezibel pro Meter (dB/m) oder der bezogene Schallleistungspegel einer ausgedehnten Schallquelle in Dezibel pro Quadratmeter (dB/m2). Obwohl es nach den für Größen geltenden Rechenregeln nicht korrekt ist, Anhängsel an eine Einheit anzubringen, um Informationen über die Art der betrachteten Größe mitzuteilen, sind solche Anhängsel beim Dezibel z. B. in den Empfehlungen der ITU[3][4] noch gebräuchlich. Wegen der Eindeutigkeit und der möglichen Verwechslungsgefahr mit Einheitenprodukten (z. B. dB•m statt dBm) sollte nach den Festlegungen in DIN, IEC und ISO-Normen diese Informationen aber stets mit der Größe selbst und nicht mit der Einheit verknüpft werden. Die geläufigsten Beispiele für dB-Anhängsel sind in der folgenden Tabelle zusammengefasst:
Darüber hinaus existiert noch eine sehr große Anzahl weiterer Anhängsel, die in verschiedenen Fachgebieten uneinheitlich verwendet werden. Für viele Pegelgrößen existieren genormte Bezugswerte. Anwendung
Die Angabe von Pegeln, Pegeldifferenzen, Pegelabständen und Maßen in Dezibel spielt in verschiedenen Fachgebieten eine Rolle. Vor allem in der Akustik und der Tontechnik, der Nachrichtentechnik und der Hochfrequenztechnik sowie in der Automatisierungstechnik haben die verwendeten Größen einen sehr großen Wertebereich. Die Angabe als logarithmische Verhältnisgröße in Dezibel erlaubt daher oft eine schnellere und anschaulichere Interpretation von Größen, da damit die betragsmäßigen Wertebereiche durch den Logarithmus auf wenige Dezimalstellen reduziert werden. Außerdem vereinfachen sich bestimmte Rechenoperationen, die in der Praxis oft vorkommen. So wird aus der Multiplikation von Verhältnisgrößen eine Addition, aus der Division eine Subtraktion. Weiterhin entspricht die Angabe von Pegeln physikalischer Größen in Dezibel eher dem menschlichen Sinneseindruck, da dieser in etwa logarithmisch zur Intensität des physikalischen Reizes verläuft (Weber-Fechner-Gesetz). Das hat vor allem für die Akustik Bedeutung, wo auch die Maßeinheit der psychoakustischen Größe Lautstärke, das Phon durch eine Verknüpfung mit dem physikalischen Schalldruckpegel in Dezibel definiert ist. Literatur
Einzelnachweise
Kategorien: Maßeinheit | Elektrische Einheit |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Bel_(Einheit) aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


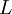 (Pegel),
(Pegel), 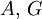 (Maße), u.a.
(Maße), u.a.
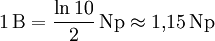



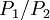
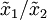
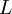
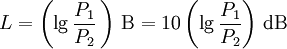 .
.
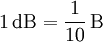 .
.
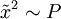 .
.
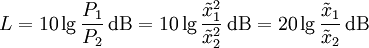 .
.
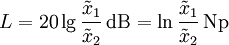 .
.
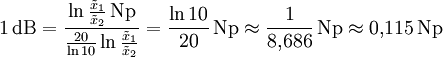 .
.