Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Bethe-Weizsäcker-Formel
Die halbempirische Formel wurde erstmals 1935 von Carl Friedrich von Weizsäcker aufgestellt. Produkt-Highlight
Formel
Für einen Kern mit N Neutronen und Z Protonen und damit einer Nukleonenzahl A = N + Z ergibt sich die Bindungsenergie EB aus den unten aufgeführten fünf Summanden. Streng genommen muss man auch die Bindungsenergie der Elektronen an einen Atomkern selbst beachten. Die Atommasse ist wegen der Bindungsenergie der Elektronen an den Kern stets etwas kleiner als die Summe aus Kern- und Elektronenmasse. Typische Elektronenbindungsenergien liegen im Bereich von einigen keV. Im Vergleich zu den Kernbindungsenergien, die im Bereich mehrerer MeV liegen, kann die Elektronenbindungsenergie jedoch vernachlässigt werden. Über die Bindungsenergie lässt sich die gesamte Kernmasse / Kernenergie m berechnen. m = Nmn + Zmp − EB / c2 mit der Ruheenergie des Neutrons mn = 939,553 MeV/c² und der Ruheenergie des Protons mp = 938,259 MeV/c². Mit dieser Erweiterung wird die Formel auch häufig Massenformel genannt. Die für den Kern erhaltene Masse lässt sich über die Beziehung E = mc2 auch durch eine Energie ausdrücken. Die gesamte Bindungsenergie eines Atomkerns setzt sich aus fünf Beiträgen zusammen:
Erläuterung der fünf BeiträgeVolumenanteil
Die Volumenenergie resultiert aus der gegenseitigen Anziehung der Nukleonen aufgrund der starken Kernkraft. Da diese aber äußerst kurzreichweitig ist, trägt immer nur die Wechselwirkung mit den nächsten Nachbarn eines Nukleons zur Bindung bei. Für ein von allen Seiten mit anderen Nukleonen umgebenes Nukleon, wie es in großen Kernen der Fall ist, ist somit die Bindungsenergie unabhängig von der Gesamtzahl der Nukleonen. Oberflächenanteil
Die Nukleonen an der Oberfläche sind von weniger Nachbarn umgeben als die Nukleonen im Inneren des Kerns. Dadurch sind sie schwächer gebunden und reduzieren die Bindungsenergie.
Der Oberflächenterm beschreibt das Verhältnis von Oberfläche und Volumen. Die Oberfläche einer Kugel ist proportional zu R2 und daher auch zu Coulomb-Anteil
Je größer ein Kern wird, desto größer wird die gegenseitige Coulomb-Abstoßung der Protonen im Kern. Da die Coulomb-Energie einer homogen geladenen Kugel proportional zu Symmetrieanteil
Dieser Term ist quantenmechanischer Natur und sorgt für ein Gleichgewicht zwischen Neutronenzahl und Protonenzahl. Er verschwindet für N = Z und schwächt die Bindung mit zunehmender Differenz zwischen Neutronen- und Protonenzahl. Da sowohl Neutronen als auch Protonen der Fermistatistik folgen, gilt das Pauliprinzip, wonach jeder Quantenzustand nur einfach besetzt werden kann. Der energetisch höchst besetzte Zustand definiert die Fermienergie. Die Symmetrieenergie sorgt dafür, dass Neutronen und Protonen dieselbe Fermienergie haben.
Paarungsanteil
gg-Kerne sind somit besonders stabil. Dies kann als Kopplung von Protonen/Neutronen zu Paaren gesehen werden, wodurch die Bindungsenergie erhöht wird. Die angegebenen Werte für die empirischen Parameter werden aus experimentell gemessenen Kernmassen bestimmt, indem die Massenformel an die Bindungsenergien von mindestens fünf Kernen angepasst wird. Je nach Wahl dieser Kerne variieren die genauen Werte in der Literatur. Dies liegt dann daran, dass die Formeln für jeweils andere Massenbereiche optimiert wurden. Eine Erläuterung zu den einzelnen Termen befindet sich ebenfalls im Artikel Tröpfchenmodell. Siehe auch: Hans Bethe, Carl Friedrich von Weizsäcker Literatur
|
|
| Dieser Artikel basiert auf dem Artikel Bethe-Weizsäcker-Formel aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





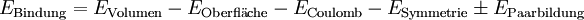
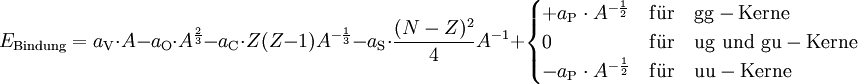
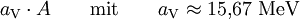

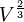 . Wegen V = A (siehe Volumenanteil) gilt
. Wegen V = A (siehe Volumenanteil) gilt 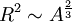 .
V.a. bei kleinen Kernen mit wenigen Nukleonen macht sich der Oberflächenanteil stark bemerkbar. Er wird mit wachsender Nukleonenzahl immer kleiner.
.
V.a. bei kleinen Kernen mit wenigen Nukleonen macht sich der Oberflächenanteil stark bemerkbar. Er wird mit wachsender Nukleonenzahl immer kleiner.
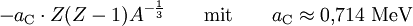
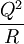 ist, ergibt sich daraus unter Berücksichtigung der oben genannten Proportionalitäten durch Einsetzen der Kernladung Z für die Ladung Q:
ist, ergibt sich daraus unter Berücksichtigung der oben genannten Proportionalitäten durch Einsetzen der Kernladung Z für die Ladung Q:
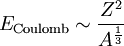 .
Dies ist auch der Grund dafür, dass Atome nur bis zu einer Ordnungszahl von 82 dauerhaft bestehen können. Durch diese Abstoßung wird die Bindungsenergie ebenfalls verringert.
.
Dies ist auch der Grund dafür, dass Atome nur bis zu einer Ordnungszahl von 82 dauerhaft bestehen können. Durch diese Abstoßung wird die Bindungsenergie ebenfalls verringert.

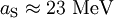 . Dort wurde die 4 aus dem Nenner mit in die Konstante eingerechnet und taucht in der Formel nicht mehr auf.
. Dort wurde die 4 aus dem Nenner mit in die Konstante eingerechnet und taucht in der Formel nicht mehr auf.



