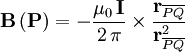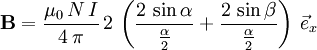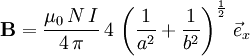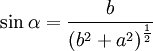Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Biot-Savart-Gesetz
Das Biot-Savart-Gesetz beschreibt das Magnetfeld, das durch bewegte elektrische Ladungen erzeugt wird. Benannt wurde es nach den beiden französischen Mathematikern Jean Baptiste Biot und Félix Savart. Es stellt neben dem Ampèreschen Gesetz über die Kraftwirkung magnetischer Felder auf bewegte elektrische Ladungen eines der beiden Grundgesetze der Magnetostatik, eines Teilgebiets der Elektrodynamik, dar. Produkt-Highlight
Experimentelles ErgebnisEin Stromleiter der infinitesimalen Länge
Das gesamte Magnetfeld ergibt sich durch Aufsummieren aller vorhandenen infinitesimalen Stücke, also durch Integrieren. Das entstehende Wegintegral kann man unter Benutzung von
Diese beiden Formeln sind strukturell sehr eng verwandt mit denen des Coulombschen Gesetzes, das die Gestalt des elektrischen Feldes in Abhängigkeit einer Ladungsverteilung beschreibt, was aber wegen der Äquivalenz von magnetischen und elektrischen Feldern nicht verwunderlich ist. In den beiden obigen Formeln wurde dabei vernachlässigt, dass die Stromleiter einen endlichen Querschnitt haben. In realen Anwendungen ist dieser im Vergleich zur Ausdehnung des Magnetfeldes aber auch tatsächlich ohne Bedeutung. Eine weitere Ungenauigkeit besteht darin, dass sich der Beitrag einer Ladung an einem Ort zum Magnetfeld an einem anderen Ort mit Lichtgeschwindigkeit ausbreitet. Der entsprechende Retardierungseffekt wird im Biot-Savart-Gesetz nicht berücksichtigt. Es ist daher nur für stationäre Ströme streng gültig und für Punktladungen in guter Näherung, sofern ihre Geschwindigkeit klein im Vergleich zur Lichtgeschwindigkeit ist. AnwendungACHTUNG: Die Formeln unten sind teilweise falsch. Diese Warnung wird gelöscht, wenn die Formeln richtiggestellt wurden. Kreisförmige Leiterschleife
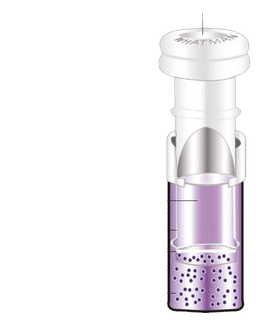
Der Betrag der magnetische Feldstärke einer kreisförmigen Leiterschleife kann mit Hilfe des Biot-Savart-Gesetzes auf der Symmetrieachse senkrecht zur Leiterschleife geschlossen angegeben werden: Dabei ist rQ der Radius der in der y-z-Ebene liegenden Leiterschleife, und x der Abstand des Beobachtungspunkts vom Zentrum der Leiterschleife. Das Feld ist in x-Richtung gerichtet. Durch Substitution: erhält man daraus
Gerader LinienleiterZur Berechnung der Flussdichte B in einem Punkt P kann man die folgende Formel anwenden: Umgelegt auf die Winkel erhält man mit wobei ρ, s und n skalar abgebildet sind (d.h. es wird nur der Betrag und nicht die Richtung berücksichtigt). Unendlich langer gerader LinienleiterFür das Magnetfeld eines geraden, unendlich langen, Leiters auf der z-Achse ergibt das obige Linienintegral
wobei ρ der senkrechte Abstand zur z-Achse und RahmenspuleNach der runden Spule ist die Rahmenspule die am häufigsten verwendete Variante. Die Formel kann aus der Formel für den Linienleiter abgeleitet werden, indem man die geraden Abschnitte der Spule als Linienleiter behandelt. mit Siehe auch
|
|||
| Dieser Artikel basiert auf dem Artikel Biot-Savart-Gesetz aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |




 am Ort
am Ort 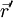 , der von einem Strom I durchflossen wird, erzeugt am Ort
, der von einem Strom I durchflossen wird, erzeugt am Ort 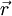 das Magnetfeld (vgl. Rechte-Hand-Regel):
das Magnetfeld (vgl. Rechte-Hand-Regel):
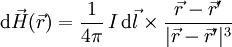 .
.
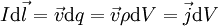 in ein Volumenintegral umformen, wobei
in ein Volumenintegral umformen, wobei 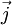 die elektrische Stromdichte ist. Somit erhält man die integrale Form des Biot-Savartschen Gesetzes
die elektrische Stromdichte ist. Somit erhält man die integrale Form des Biot-Savartschen Gesetzes
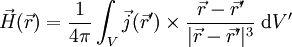 .
.
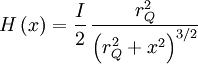
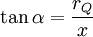
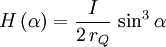
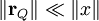 Kann das Feld der Leiterschleife als
Kann das Feld der Leiterschleife als 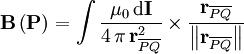
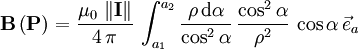
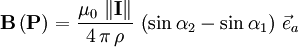
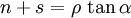
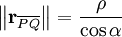
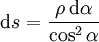
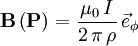 ,
,
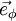 der Einheitsvektor bezüglich des Winkels
der Einheitsvektor bezüglich des Winkels